Happy 12th of December!
Throughout the month, to accompany the release of our book on the Mathematics of Christmas, Hannah Fry & I are tweeting out Christmathsy bits and pieces, one a day, advent calendar style. Assuming we don’t run out of ideas, that is…
As you’ll have gathered, one of the fundamental principles of our book is the absolute and unquestionable truth of Santa’s existence. However, even if you know that the big fellow is real, that doesn’t necessarily mean he’s easy to spot. For example, one of these three is Santa… but which one?
Answers via the comments or on Twitter. All correct answers will be rewarded with deep respect and warm Christmas wishes. Enjoy!
CLICK HERE TO SEE THE WHOLE CALENDAR SO FAR
SOLUTIONS TO PREVIOUS PUZZLES
Click here for Sunday’s puzzle.
Click here for Friday’s puzzle.
Scroll down for the solutions…
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Solution to Sunday’s Puzzle:
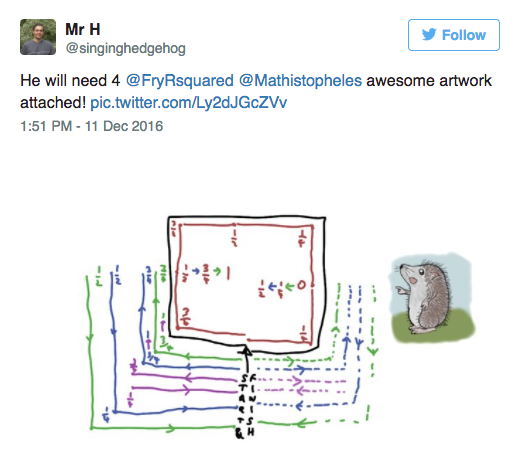
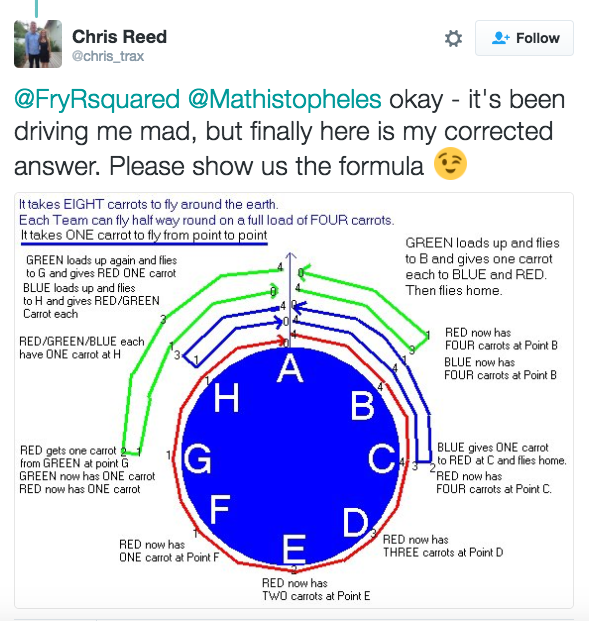
Santa needs two additional teams to fly around the world:
- Santa and the two teams (A and B) set out together to 1/8 of the way round the world.
[At this point, all three have 3/4 of a tank of carrots left.] - B transfers 1/4 of a tank to Santa and 1/4 of a tank to A.
[Now, Santa and A have full tanks; B has 1/4 of a tank.] - Santa and A fly on to 1/4 of the way round the world; B returns to Lapland.
[Now, Santa and A have 3/4 of a tank; B refuels to have a full tank.] - A transfers 1/4 of a tank to Santa.
[Now, Santa has a full tank; A has 1/2 a tank; B has a full tank.] - Santa flies on to 1/2 way round the world; A returns to Lapland.
[Now, Santa has 1/2 a tank; A refuels, so A and B have full tanks.] - Santa flies on to 3/4 of the way round the world; A flies 1/4 of the way round the world in the opposite direction to meet him.
[Now, Santa has an empty tank; A has 1/2 a tank; B has a full tank.] - A transfers 1/4 of a tank to Santa.
[Now, Santa and A have 1/4 a tank; B has a full tank.] - Santa and A fly to 7/8 of the way round the world; B flies 1/8 of the way round the world in the opposite direction to meet them.
[Now, Santa and A have empty tanks; B has 3/4 of a tank.] - B transfers 1/4 of a tank to Santa and 1/4 of a tank to A.
[Now, all three have 1/4 of a tank.] - Santa completes his journey, accompanied by the two support teams.
Phew!
Well done to Matthew Smith in particular (see the comments on the puzzle), who posted pretty much precisely this answer, the most complete correct answer that I think we received.
The puzzle was from the great Martin Gardner, and we have also discovered that, coincidentally, it was also covered very recently here.
Thanks for all the diagrams, whether correct solutions or not! Some examples:
PS. And a late (brilliant, correct) entry!
Solution to Friday’s Puzzle:
Santa can fit 10 elves into the room. There are various ways of doing this. Here’s one of them:
The puzzle itself is a variant of the Eight Queens Puzzle, which asks how you can place eight queens on a chess board such that no two queens threaten each other. Elves are like queens, but with slightly worse eye-sight, which allows you to squeeze in a couple more!
You can prove that 10 is the maximum by considering the diagonals of a particular colour:
Suppose you had a solution with more than 10 elves; then one or other colour of tiles would necessarily hold at least 6 elves. Suppose it was the darker tiles (since the argument would be the same with the lighter ones).
In the diagram above, there are seven diagonals of dark tiles running SW-NE (there are more running SE-NW but that’s not relevant). Since no diagonal may have more than one elf, and we are supposing that the dark tiles have at least six elves, at least six of these diagonals must have an elf. All you have to do from here is to prove that this is not possible.
Since the board is symmetrical, there are only four cases to consider: Can six elves be placed on these diagonals, omitting, in turn, the first, second, third or fourth diagonal? If you consider each of these cases systematically, you’ll find that the answer is no (this is relatively quick to do, since many of the placements are forced until you reach a point where it is impossible to place an elf). I won’t go through the process here – it’s a little tedious – but you can either take my word for it or verify for yourself.
As far as I can tell, the only person [EDIT: I was wrong – see the PS!] to submit a correct answer was Matthew Smith (again!), via the comments on the puzzle page:
This explanation sounds pretty similar to my approach above, though Matthew considers all the diagonals rather than those of one colour. You can see his proposed solution by clicking on the comment.
Hearty congratulations definitely in order!
P.S. A second special mention for the daughters of Bill Finch (10 & 12), who showed how to maximally fill eight rows of an extended room, a solution that could be repeated on the next 8 rows up (if shifted to the right by enough tiles) and so on to continue to place elves indefinitely in an infinitely expanding room:
FWIW, Here is their extended pattern, demonstrating that you can get no more than 16 in any one direction… pic.twitter.com/SPkn7NisiY
— Bill Finch (@Billfinch1118) December 12, 2016






About the solution to the Elfnigma. I see which thoughts could have put me on a better track:
1. Putting as many elves to borders would leave more free room for further elves
2. thinking about using as few as possible diagonals ideal positioning of one elf could be in a corner, but two elves with an offset one aside only occupy two diagonals leaving the longest diagonal for a third elve, very economical.
If you start with thought 2 the rest of the elves almost fall into place automatically in knight moves creating the cross b8,d7,f6,h5 and g8,f6,e4,d2 leaving two more gaps on column a.
A last word on Elfnigma: As the german word for 11 is Elf, I am disappointed only 10 elves fit in.
Pingback: Imp and Pixie Puzzles | Mathistopheles