SOLUTION
In this sequence, the nth term is the smallest positive integer (other than 1) that can be expressed in all bases from 2 to n using only the digits “1” and “0”.
Specifically:
- TERM 1
Base 1 does not exist.*
The first term is not defined.
.
- TERM 2
In base 2, every number consists only of “1” and “0”.
The second term is 2.
. - TERM 3
2 is ‘2’ in base 3, so that is no good.
3 is ‘11′ in binary AND ‘10′ in base 3.
The third term is 3.
. - TERM 4
2 is ruled out, because we already know that 2 is ‘2’ in base 3.
3 is ‘3’ in base 4, so that is no good either.
4 is ‘100′ in binary, ‘11′ in base 3 and ‘10′ in base 4.
The fourth term is 4.
. - TERM 5
82000 is ‘10100000001010000’ in base 2, ‘11011111001’ in base 3, ‘110001100′ in base 4 and ‘10111000’ in base 5. There are no smaller numbers with the desired property.
The fifth term is 82000.
This sequence struck me as particularly intriguing. It seems to be plodding along in a fairly pedestrian fashion: 2, 3, 4, … before suddenly jumping four orders of magnitude to 82000, a number that feels particularly jarring because it is almost obstinately unremarkable. 82000 is not a number that turns up in a lot of different contexts; as a rule, it keeps quite a low profile, and yet here it is popping up in our sequence, seemingly out of nowhere.
Moving forward, 82000 is big, but it is not so big as to make you lose hope that finding another term might also be manageable. How many digits might the sixth term (the first number that is expressible with only “0” and “1” in bases 2, 3, 4, 5 and 6) have? Ten? Twenty? More than that?
THE SIXTH TERM
To find the fifth term, I had written a program in Python. Essentially, it worked by going through all the positive integers in binary, treating their digits as those of a base six number, then expressing that number in bases 3 through to 5 to check whether these other expressions contain only “1” and “0”. Probably not the most efficient way of doing things, but given that it had worked well enough so far (finding 82000 in under a second), I was hoping to find the next term in relatively short order.
A couple of hours of computer time later… nothing. The program had checked values up to 204698073815493849907 (‘111111111111111111111111111’ in base 6), but it had not found any solutions, indicating that, if the sixth term exists, it must be greater than 1021.
I probably should not have bothered looking at all. Although this sequence is not in the rather fabulous On-line Encyclopedia of Integer Sequences [UPDATE: It is now.] the sequence of “Numbers that can be written from base 2 to base 5 using only the digits 0 and 1” (Sequence A146025) is. This sequence reads “0, 1, 82000″… and that is that. With three terms, the sequence is “conjectured to be complete” and has apparently been checked to 3125 base 5 digits (i.e. to roughly 102184, which somewhat puts my 1021 in the shade).
Obviously, the sixth term of our sequence would also have to be in Sequence A146025. Therefore, since 82000 itself is no good (82000 is ‘1431344’ in base 6), the sixth term must have over 2000 (base 10) digits, if it exists at all (over 2184 digits, in fact).
WHY THERE MAY BE NO MORE TERMS
I do not have a proof as to whether or not there are any more terms in the sequence. However, I do have the following loose argument, which I feel is at least suggestive that we may already have found all there is to find.
Let’s take an extremely naive view and suppose that the digits of any d-digit positive integer n, expressed in base b, can be considered to be randomly and independently selected from the b possible digits used in that base (with the exception of the first digit, which is additionally constrained not to be zero). In this case, the probability that n is written only with 1s and 0s in base b would be equal to:
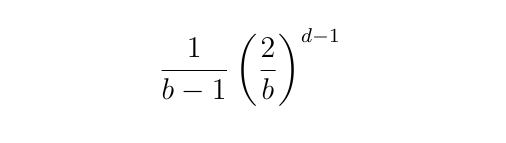 The relationship between n and d, the number of digits of n in base b, is:
The relationship between n and d, the number of digits of n in base b, is:
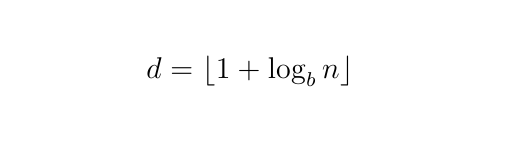 So, if we further assume that the digits of n in different bases can be considered to be independent (I will come back to these dodgy assumptions!), then the probability p(n,b) that n is written only with “1” and “0” in all bases from 2 to b would be equal to:
So, if we further assume that the digits of n in different bases can be considered to be independent (I will come back to these dodgy assumptions!), then the probability p(n,b) that n is written only with “1” and “0” in all bases from 2 to b would be equal to:
The expected number e(b) of positive integers (greater than 1) that can be expressed in all bases from 2 to b using only the digits “1” and “0”, could then be found by adding up these probabilities, from 2 to infinity:
Now, I do not want to go into all the tedious manipulations, but it turns out that with a bit of messing around, you can show that this expectation is bounded above and below in the following way:
where:
Now, the key question is whether the infinite sum in those bounds on e(b) converges or not, for each value of b. If it does converge, then (given our very shaky set of assumptions) we would expect there to be a finite number of integers (possibly none at all) that could be expressed with only “1” and “0” in bases 2 through to b. If it does not converge, then we would expect there to be an infinite number of such integers.
Luckily, it is well known that those sums converge if and only if the exponent α(b) < −1. Hence we just need to check the value of α(b) for each integer:
- α(2) = 0 > −1. Therefore e(2) = ∞.
This is what we would expect, since we know that every positive integer (i.e. an infinite number of positive integers) is expressible using only “1” and “0” in binary.
. - α(3) ≈ −0.37 > −1. Therefore e(3) = ∞.
Again this is what we expect because there are an infinite number of positive integers expressible using only “1” and “0” in base 3, and all of them are also expressible using only “1” and “0” in binary.
. - α(4) ≈ −0.87 > −1. Therefore e(4) = ∞.
This suggests that there are an infinite number of positive integers expressible using only “1” and “0” in bases 2 through to 4 (which seems to fit with this sequence).
. - α(5) ≈ −1.44 < −1. Therefore, the sum converges, e(5) is bounded above and below by finite values, so e(5) is itself finite.
This suggests that there are a finite number of positive integers expressible using only “1” and “0” in bases 2 through to 5.
In fact, for b = 5, that infinite sum is equal to about 1.89. Substituting this into the upper and lower bounds for e(5) suggests that the expected number of positive integers (greater than 1) expressible with only “1” and “0” in bases 2 through to 5 should lie between 0.08 and 0.59. In other words, even the fact that there is one number like this (82000) might be counted as quite a lucky result. It would be reasonable to conclude that there are likely to be no others, and if there are no more positive integers of this kind, then there certainly aren’t any positive integers (greater than 1) expressible with only “1” and “0” in bases 2 through to 6. This would mean that 82000 was the last number in our sequence.
[UPDATE: Hacker News commenter throwaway_yy2Di has created a nice graph of my upper and lower expectation bounds for values of b from b = 2 to b = 15.]
Clearly, there are significant issues with this argument. The digits of a particular number in a certain base are not chosen randomly, nor are they generally independent from one base to another. A number that ends in a “1” in base 6 will also end in a “1” in base 3, for example.
On the other hand, I do feel that there is something going on here. After all, 3, 4 and 5 are the only bases that are actually relevant to the argument given above and they have no common factors (unlike 3 and 6 in the example given above). If you pick a moderately large positive integer that is expressible using only “1” and “0” in base 5, wouldn’t you expect the base 3 and base 4 representations of that number to look as if their digits had been chosen randomly and independently?
Also, it is worth observing that our supposed probability p(n,5) that a given integer n will be expressible with only “1” and “0” in bases 2 through to 5 actually drops off quite quickly. Most of the expectation of finding solutions is concentrated around the lower integers (the bigger n gets, the more digits have to fall our way), so if you have got to 102184 and you still have not found a solution…
AN OPEN PROBLEM
Anyway, that is the best I can do. I do not think there are any more terms in the sequence, but it is an open problem, so I would be delighted to see whether anyone else has any ideas on how this could be investigated. Comments are welcome, as always.
UPDATE: The 82000 sequence seems to have captured the imagination of quite a number of people. I have collected some links to related content HERE and HERE. I have also posted some ideas on related sequences HERE.
* Note that, while the “unary” system, in which positive integers are represented by a sequence of 1s (a tally system, essentially) is sometimes referred to as “base 1”, it is not a mathematically natural extension of what “base n” means for all other positive integers. Since I am interested in the mathematical properties of this sequence, it is important to use a mathematically consistent definition. Hence, the statement that “base 1” does not exist, since there is no true positional numbering system that uses only one distinct digit.
Thomas Oléron Evans, 2015


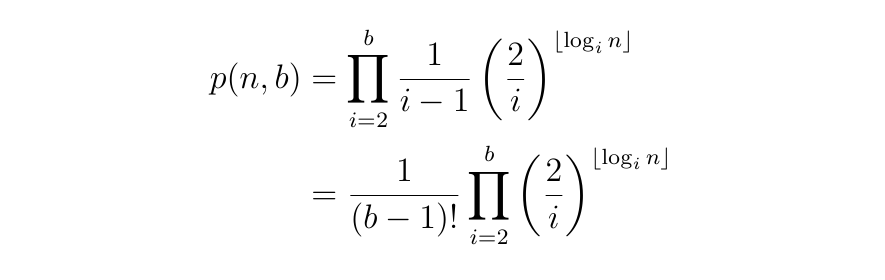
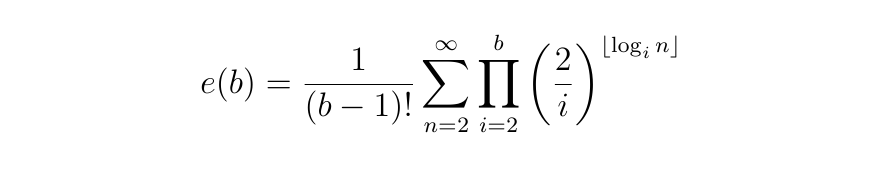
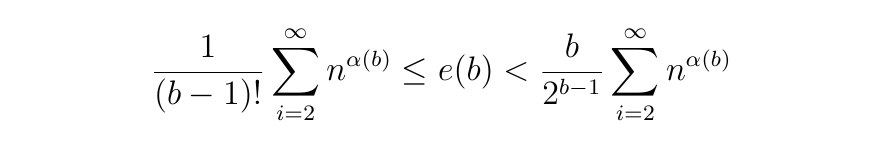
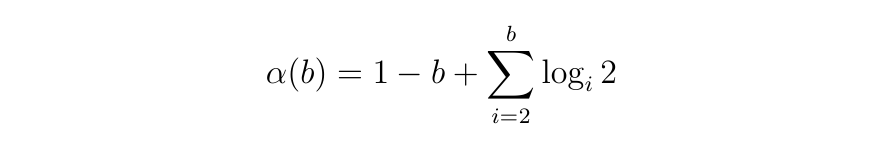
I’ve written some base conversion software that may be useful in helping search efficiently. I would like to chat more if that would be interesting to you.
By all means continue the search; I’m glad this has gained some interest. I don’t intend to continue working on this problem myself though. If you have any more thoughts on the problem, please do post them here or contact me on Twitter.
Hi,
If you represent a number in base 2. The probability of the last digit being 1 is 1/2.
For base 4, the probability of the last digit being 0 is 1/4.
So, thinking along the same line as your argument, the joint probability for these two events is 1/8.
But this 0, because the first event tells us the number is odd, whereas the second event tells us it’s even.
Maybe the question will become easier/more interesting, if you restrict the bases to primes up n.
I agree that the digits are not truly independent. It is a heuristic argument, not a precise one. Using only primes would not help, though, because if all of your other digits obey the 0, 1 condition, you will always have an even-odd dependence issue with the final digit. The question is whether the assumptions are close enough to the reality of the situation to make the conclusions meaningful.
If you look at the probabilities associated with base 2, all of them are 1 (as you would expect, since every number in base 2 is necessarily expressed with only 1 and 0). The products could start from i = 3 and the calculation would be unaffected. The three bases that we are left with in the main calculations, 3, 4 and 5, have no common prime factor, so I don’t think the dependencies should damage the argument that much. I could well be wrong though.