This post is about the mathematically perfect way to organise your office Secret Santa, as discussed in a new book that I have written with Dr Hannah Fry: “The Indisputable Existence of Santa Claus: The Mathematics of Christmas”.

Ah, Secret Santa. Two words guaranteed to conjure up a veritable sleighload of festive thoughts in the minds of office workers up and down the land. Thoughts like “obligatory”, “awkward” and “How can I make this look more expensive?”

Unfortunately, despite Secret Santa’s uniquely vital role in making people feel unknown and undervalued among their colleagues, mathematically it’s a total mess. Here’s Hannah Fry, explaining exactly what’s wrong with it and presenting our all-new Super Secret Santa system:

So there you have it; a mathematically perfect Secret Santa. Christmas is saved.

Except… as some people have pointed out (and as we acknowledge in our book, to be fair), the system we propose isn’t quite perfect. Here’s why…

In the book, we demand that a perfect Secret Santa system should be:

• Transparent – People pick their own giftee out of a hat;
• Fair – Everyone is equally likely to be matched;
• Efficient – There is never any need for redraws;
• Secret – No one has any information about who is more likely to be matched, including the organiser.

As Hannah explains in the video, the usual Secret Santa system, putting all the names in a hat and having everyone draw someone to buy for, fails on three out of four of those criteria: fairness, efficiency and secrecy.

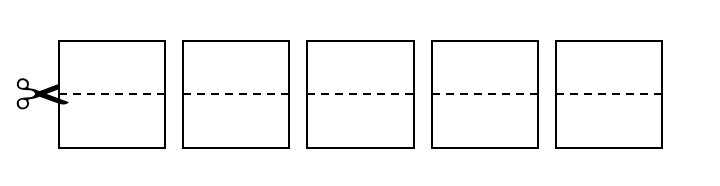
With our alternative method, the organiser creates a series of cards like this, one for each participant, with the same number top and bottom, but with different numbers on each card:

The cards are then turned over, shuffled and laid out in a row, and each card is cut along the middle, separating the top and bottom halves but still keeping the order secret:

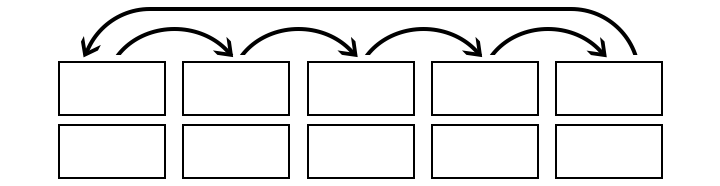
The top halves of the cards are then shifted one place to the right, with the top of the last card being moved back to the start.

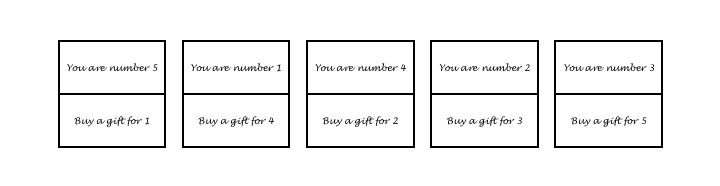
The tops are then reattached to the new bottoms (with sellotape, for example), creating a set of cards in which every participant will be allocated to buy for someone other than themselves (mathematically speaking, we have created a derangement of the participants). Of course, you mustn’t look at the cards (!), but here’s what they might look like now:

These cards go into a hat, and everyone picks one out. Then each participant writes their name against their number on a list that you should have remembered to stick up on a noticeboard somewhere nearby:

Now, we’re pretty pleased with this system. No redraws needed (perfect efficiency), everyone equally likely to pick everyone else (perfect fairness), and everyone gets to pick from a hat (perfect transparency), much better than one of those joyless online allocation systems.

It’s practically perfectly secret as well. Once everyone has drawn, unlike the standard Secret Santa method, no one has any idea about who is buying for who. No idea at all. Almost.

Because, as some pedants* have noted, our method can never result in two people buying presents for each other**… Which means that once you find out who you are buying for, you have some information about who might be buying for you; you know it’s not the person you’ve drawn yourself.

So yes, strictly speaking this violates our secrecy condition. But isn’t this a feature, rather than a bug? Do we really want people to be buying for each other? After all, if they found out, they might agree to get each other presents they actually wanted, and where would we be then, eh?

But all right, all right. We did actually consider this issue in advance and we do have a solution. I have to warn you though, pedantry has its consequences. If you really want to go through with this, it’s going to take you a while…

CLICK HERE FOR THE METHOD

---

* Don’t get me wrong, I’m not using “pedant” as an insult. I’m a mathematician, I love pedantry!

** Unless there are only two participants, in which case I don’t think you can really call it Secret Santa now, can you…

---

Thomas Oléron Evans, 2016