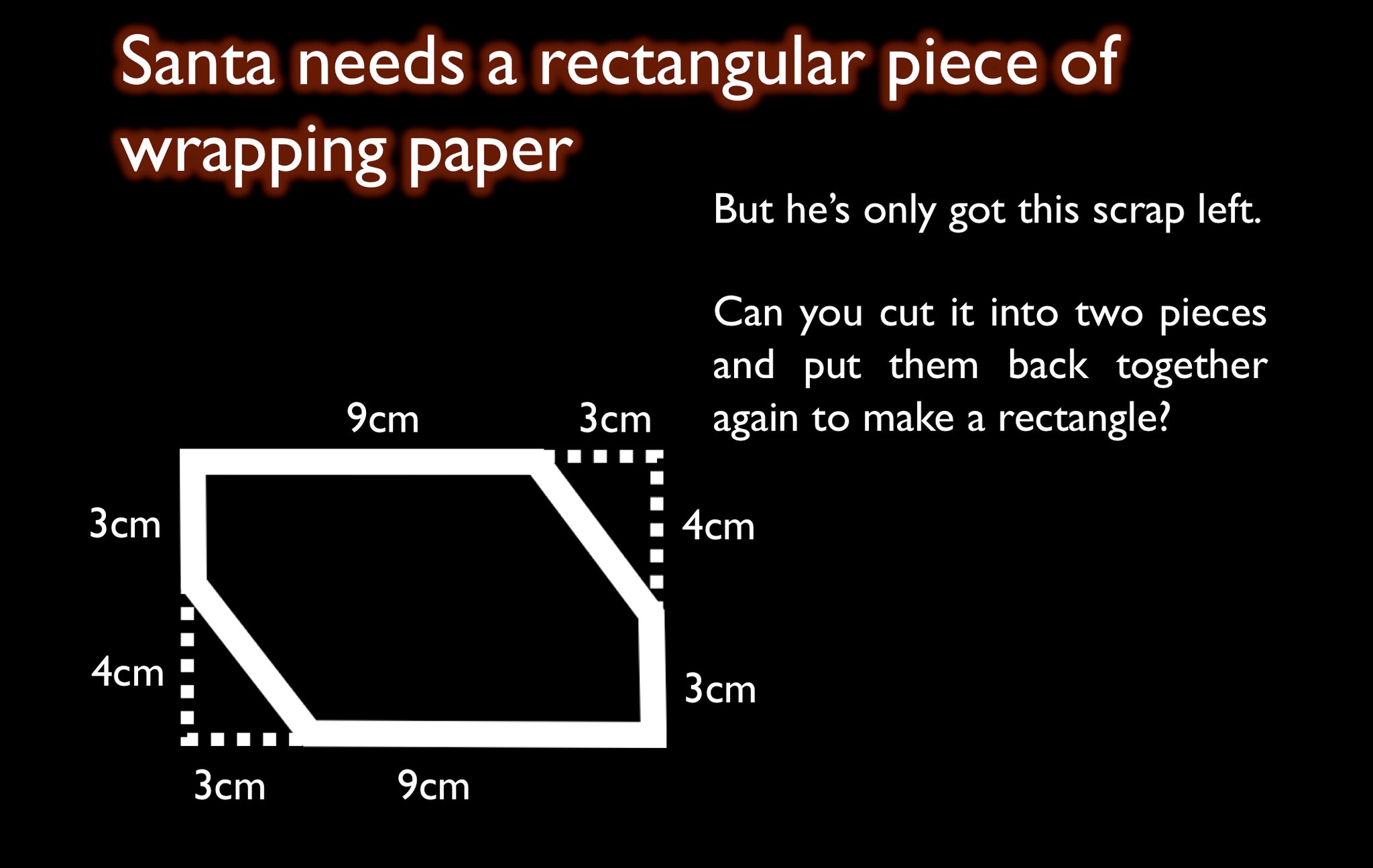
Happy 13th of December!
Throughout the month, to accompany the release of our book on the Mathematics of Christmas, Hannah Fry & I are tweeting out Christmathsy bits and pieces, one a day, advent calendar style. Assuming we don’t run out of ideas, that is…
Answers via the comments or on Twitter. All correct answers will be rewarded with deep respect and warm Christmas wishes. Enjoy!
CLICK HERE TO SEE THE WHOLE CALENDAR SO FAR
SOLUTION TO YESTERDAY’S PUZZLE
Scroll down for the solution…
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Solution:
The real Santa was the middle one.
Left-Santa can’t be telling the truth, so at least one is telling the truth. Middle-Santa can’t be lying, since that would imply he was telling the truth about there being at least two liars. So Middle-Santa is telling the truth, which implies Right-Santa is lying (along with Left-Santa). This means that Santa never lies, so Middle-Santa must be the real one.
Congratulations to Tim McDonald, Pierre Schramm, Stuart Langridge, Andrew Wyld, Troy, Pupang and Olaf Doschke, who all got it right, Also, a special mention for Katie, both for this observation:
[Take a look back at the image… She’s got a point, you know.]
… and for this wholly reasonable question:
Katie is right to remark that we are implicitly assuming that all the statements must have a well-defined truth value. Technically, it’s not actually that the one on the left CAN’T be the real Santa; it’s just that if he is then the statements are not consistent (or not well-founded in a logical sense).
Thanks for all the contributions!


>it’s not actually that the one on the left CAN’T be the real Santa; it’s just that if he is then the statements are not consistent.
With that argument anyone making an inconsistent statement could render someone else unreal? Why didn’t Hillary Clinton think of that?