In mathematics, using the right language is important. Many of the catchy phrases people tend to remember from school maths lessons – “change side, change sign”, “two minuses makes a plus” or “BIDMAS” (or “BODMAS” or “PEMDAS”; choose your poison) – can lead to damaging misconceptions, since they don’t reflect what is really going on mathematically when the rules they describe are applied (see those links for details).
This sort of problem is not restricted to the English-speaking world though. In France, one particular example of mathematical imprecision seems to have managed to slither its way into everyday usage: the kilomètre-heure.
In English, if we wanted to describe the speed of our car, we would say that we are travelling at so-many “miles per hour”. On those rare moments when we are dragged kicking and screaming into the modern world* and forced to use the metric system, we would instead say “kilometres per hour”. In France though, it is common to refer to these units as “kilomètre-heures”.
I have always found this troubling, because, well… it’s wrong. Speed is measured in units of distance over time. Kilometres per hour means km/h (or km·h−1); the time part of the unit is inverse. You’re measuring the number of kilometres covered in each hour. The kilometres and the hours do not have the same status.
The French terms “kilomètre par heure” and “kilomètre à l’heure” express this correctly, but the very commonly used contraction “kilomètre-heure” does not. While it’s true that the unit is sometimes written as “kilomètre/heure”, this is not much comfort since it doesn’t make the verbal usage any less insidious.

While running at over 35 km/h, French sprinter and Rio 2016 200m Bronze medallist, Christophe Lemaitre, suffers a sudden moment of existential doubt over the nature of speed, caused by the imprecision of the French language. Probably.
Obviously, I’m not claiming that this issue is preventing the entire population of France from understanding the concept of speed, but just like the English examples mentioned earlier, if language is used incorrectly, it leads to subtle misconceptions that can interfere with learning and cause problems later on when encountering new concepts that require deeper understanding.**
If you put two units together – as with “kilometre hour” (let’s use the English from now on) – you are creating a compound unit in which the two basic units are multiplied, not divided. It’s easy to imagine that if you learn to interpret “kilometre hour” as km/h, rather than the correct km·h, you could make mistakes when you come across genuine multiplied units like newton metres (N·m) or kilowatt hours (kW·h).
However, there is nothing intrinsically wrong with the idea of a kilometre hour. Scientifically, it is a perfectly valid unit; it’s just not a unit of speed. So what exactly is a kilometre hour? And what might you use it for?
Something measured in kilometre hours would have to have both a (linear) spatial component and a time component. In other words, you would use a kilometre hour to measure something where you’re interested both in how long it is, and in how long it lasts.
So let’s take a trip to the seaside…
Imagine you are sitting on a narrow beach, with sea on both sides (like this). As you are sitting there, enjoying the sun, a turtle sticks it’s scaly head out of the water on one side of the beach and begins to drag itself slowly across the sand towards the sea on the other side. Immediately behind this turtle is another, then another and another, until soon, a whole parade of turtles is making its way across the beach, nose to tail.***
It really is quite a spectacle, so you sit and watch enchanted until the very last turtle in line has crossed the beach and disappeared beneath the waves. A wonderful and unexpected experience… but exactly how much turtle-based enjoyment have you had?
In order to measure your reptile watching experience, you need to consider both the length of the queue of turtles you saw and how long you were able to spend watching it; there is a spatial dimension and a temporal dimension. So linear-trans-littoral-chelonian-migratory-observation is an activity that lends itself perfectly to measurement in kilometre hours!
To experience a kilometre hour of turtles, you could watch a kilometre-long line of turtles for an hour, of course (if you could see them all at once), but you could also watch a metre-long line of turtles for a thousand hours. Or ten kilometres of turtles for six minutes. All these cases provide the same overall quantity of turtle watching: exactly one kilometre hour.
So what about our idyllic seaside scenario then. How many kilometre hours of turtles did you see?
Let’s suppose that the width of the beach is W km, the length of the queue of turtles is Q km, and the turtles crawl at a speed of V km/h.**** To keep things simple, we’ll also suppose that Q > W (i.e. the queue of turtles is longer than the width of the beach). Oh, and we’ll definitely ignore the effects of the tide – this is a magical beach of constant width.
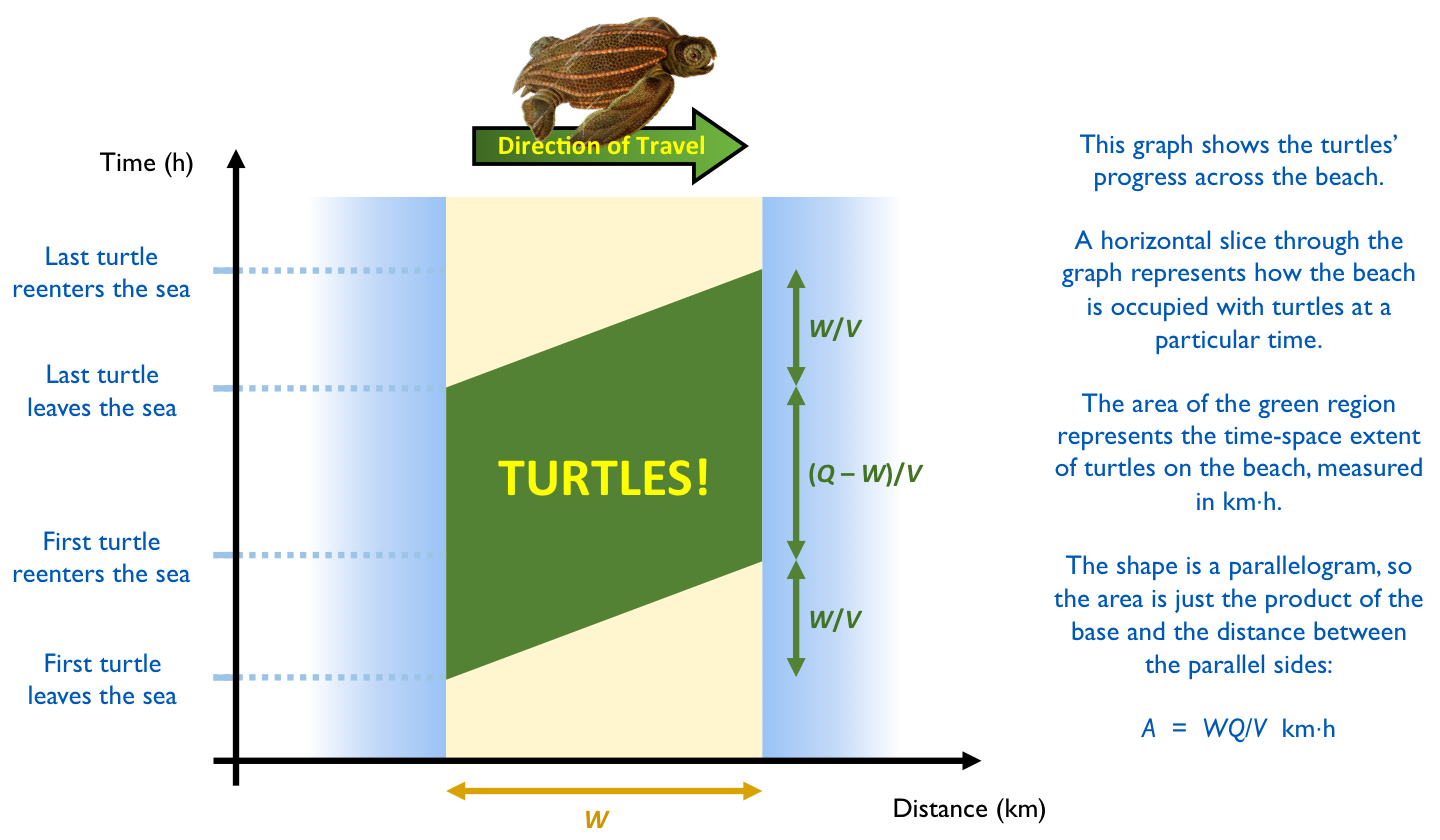
There are three stages to your experience. The first stage begins with the appearance of the first turtle and ends when it reaches the other side of the beach, at which point there is a continuous line of turtles stretching from one side to the other. This stage lasts W/V hours (the time it takes a turtle to cross the beach) and the mean length of turtles that you can see over this period is W/2 km (none at the start, the whole width of the beach by the end). This equates to W2/(2V) km·h of turtles.
The second stage lasts from the moment the first turtle finishes crossing the beach and disappears into the sea to the moment the last turtle has left the water and begun its trek across the sand. This stage lasts (Q − W)/V hours (Q − W km is the length of the queue that had not yet left the sea) and you can see a full W km of turtles throughout. This equates to W(Q − W)/V km·h of turtles. We’ll expand the brackets to rewrite this as WQ/V − W2/V km·h.
The third stage lasts from the the moment that the final turtle begins its journey across the beach, to the moment it disappears into the sea, at which point all the turtles are gone. This stage is essentially the same as the first stage, but in reverse, so it also equates to W2/(2V) km·h of turtles.
In total then, you have observed:
= W2/(2V) + WQ/V − W2/V + W2/(2V) km·h
= WQ/V km·h of turtles!*****
To put some numbers to that, with a 10 metre wide beach (W = 0.01) and a ninety metre line of turtles (Q = 0.09), which crawl at 0.25 metres per second (V = 0.9), you could look forward to (0.01 × 0.09) / 0.9 = 0.001 km·h (or 1 m·h) of turtley goodness.
Kind of funkily, this result is equal to the area that our line of turtles sweeps out in a time-space diagram of their epic journey:
We can also do a sanity check on our method of turtle measurement****** to verify that it is in some way meaningful. Provided that the turtles crawl at the same speed, we should observe the same amount of them no matter how they choose to cross the beach. For example, if they were to line up parallel with the shore and all cross simultaneously, that should also result in WQ/V km·h of turtle watching.*******
This alternative scenario is easier to analyse than the first one. Since all the turtles leave the sea and reenter it together, we observe the full length of the line, Q, throughout, while the time taken to cross the beach is W/V. This again equates to WQ/V km·h of turtles, so our method has passed the sanity check; kilometre hours really are a good way to measure turtle watching!
As it turns out, kilometre hours are actually used to measure some other (less ridiculous) things too, such as ‘fishing effort’, ‘traffic jam gravity’ and border surveillance.
I think I prefer the turtles though.
* If by “the modern world” you very charitably mean “anything after the eighteenth century“.
** Here is a nice article on children’s misconceptions of simple mathematical concepts.
*** Following the long and proud traditions of educational examples in applied mathematics, I have carefully chosen this scenario to be superficially similar to the migration behaviour of sea turtles, while simultaneously making sure that it is utterly divorced from reality in any meaningful sense.
**** Given the scenario, it would probably be more sensible to use metres and seconds, rather than kilometres and hours, but I’ve made my bed now.
***** You can actually show that the result is the same if Q ≤ W, i.e. if the queue of turtles is shorter than or equal to the width of the beach. I won’t spoil the fun by doing it here though, since I’m sure you’re already off sharpening your lucky algebra pencil.
****** I realise that you’ve probably already been questioning my sanity for several paragraphs now.
******* We have sort of thrown in the assumption that the turtles are perfectly circular here – or perhaps square – since we’re supposing they form a line of the same length whether they stand nose-to-tail or side-by-side. Unless they sidestep across the beach, of course, like some sort of synchronised reptilian dressage.
IMAGES:
Hatchling Loggerhead Turtles – Hila Shaked – Creative Commons
Christophe Lemaitre – Fernando Frazão/Agencia Brasil – Creative Commons
Turtle Illustration – Ernst Haecke – Public Domain
Turtle Head at Colchester Zoo – William Warby – Creative Commons
Thomas Oléron Evans, 2016