FIRST SET STRUGGLES

Although Serena Williams eventually triumphed at Roland Garros to win her twentieth Grand Slam title, over the course of the tournament, she did not make her life easy. In the semi-final, played two days earlier, she had dropped the first set against her opponent, twenty-third seed Timea Bacsinszky, before storming back to rescue the match in dramatic fashion. Remarkably, despite being the top seed and a very strong favourite for the title since day one, that was the fourth time that Serena had found herself in such a position in the tournament, having also lost the openers of her second, third and fourth round matches, giving her a pretty ropey first set record of “Played 7, Won 3”.

By contrast, prior to the semi-finals, the four semi-finalists in the men’s draw (Stanislas Wawrinka, Jo-Wilfried Tsonga, Novak Djokovic and Andy Murray) had between them managed to win all twenty of the opening sets that they had played. But just how costly is it to lose a set in a tennis match? And how does the value of a set differ between the women’s game (in which matches are the best of three sets) and the men’s (in which they are the best of five*)?

WHY MATHEMATICIANS LIKE TENNIS

Tennis is a fascinating game from a statistical point of view, because the mechanics of its scoring system – in which points build into games, which build into sets, which build into the overall match result – lead to a great deal of interesting permutations. For example, it is well known that you can win a tennis match while scoring fewer points than your opponent (as few as 37.2% of the points for women and 35.2% for the men**, as explained HERE***), a scenario that does indeed arise fairly frequently.

Also, calculating the probability of winning a tennis match given the probability that you will win any given point is not an entirely straightforward procedure, owing to the possibility of indefinitely long sequences of deuces and suchlike. However, if you do do the sums, you discover that tennis is a sport that massively multiplies up advantage; if you are slightly more likely to win each point, then you are quite a bit more likely to string together enough points together to take a game. This, in turn, means that you are quite a lot more likely to win a set, and ultimately very, very much more likely to claim enough sets to win the match (see THESE GRAPHS, for example). At least, that would be the case if it were not for the very significant advantage enjoyed by the serving player, which broadly has the effect of levelling everything out again, thus facilitating the odd ridiculous Isner-Mahut-style stalemate (as explained HERE).

CALCULATING THE VALUE OF A SET

To get back to our original question, calculating the value of a set is not a straightforward thing to do, because the change in a player’s probability of winning a tennis match that results from dropping or gaining a set depends heavily on their own ability and the ability of their opponent. Tennis is not like chess, say, where the value of every situation can theoretically be calculated precisely.**** In chess, once you have decided to make a particular move, you can be pretty certain that you will be able to carry it out perfectly. You are unlikely to miss the square that you are aiming for and opponents rarely throw pieces back across the table at you, so everything can be reduced to an orderly consideration of the possible strategies and their consequences, without worrying about the complicated roles of chance and physical skill.

Some pretty detailed work has been done on trying to track how a player’s probability of victory changes throughout the twists and turns of a tennis match. However, we do not have to do very complicated calculations to gain some understanding about the value of winning a set in the men’s and women’s games. Let’s see how far we can get with a much simpler approach.

First of all, let’s not worry about points and games. That would be too much of a hassle. Instead, in a match between Players A and B, we will assume that there is a certain fixed probability P that Player A will win any given set (so the probability that Player B wins the set would be 1 − P) and that the results of each set are completely independent. It seems to me that these assumptions are actually a good deal more reasonable than supposing that there is a fixed probability that a player will win any given point (used in some of the links above), because we know that there is a big difference between serving and receiving, but this difference should even itself out over the course of a complete set, owing to the fact that players alternate their service games and that they need to win by two clear games (or by two clear points, in a tie-breaker).

The absolute simplest thing to do would be to assume that the players are evenly matched, each with a 50% chance of winning any set (P = 0.5), so let’s start by doing that. We can think of this as the approach that involves the minimum possible knowledge about the players. If we do not know anything about who is playing, then it would not make sense to suppose that either of the players has any particular advantage over the other.

We want to know how winning or losing the first set affects a player’s chances of winning the match. Since all sets are worth the same amount, these calculations will actually tell us about the value of any set, but the argument is easier to follow if we think about the first set specifically, given the complication that later sets might not actually be played.

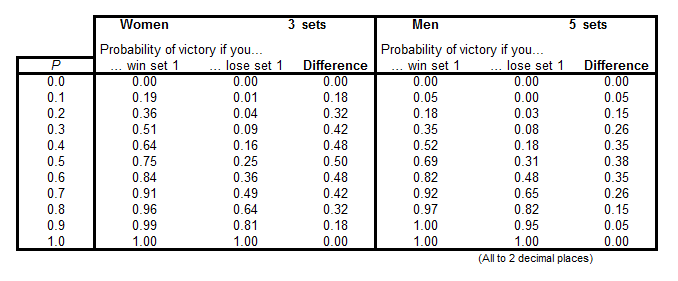
Let’s take the women’s game first. If a player loses the first set, then they must win both of the remaining sets to win the match. The probability of doing this is 0.5.×.0.5.=.0.25 or 25%. If, on the other hand, they win the first set, then they must win at least one of the remaining sets. The probability of this happening is equal to 1 minus the probability that they lose both of the remaining sets, which is 1 − 0.5 × 0.5 = 0.75 or 75%. So, in this case, you are three times more likely to win a match if you win the first set than if you lose it. The result of a particular set, independent of all other results, affects your probability of victory by a difference of 0.5, or 50 percentage points.

Now the men’s game. If a player loses the first set, then they must win at least three of the remaining four sets to win the match. It makes the calculation easier if we assume that all five sets are played, whatever the results in the earlier ones. This is a perfectly valid thing to do, because playing out these sets would have no effect on the result of a match.

The probability of winning three of the remaining four sets is equal to the probability of winning exactly three of them plus the probability of winning all four. There are four ways to win precisely three sets (because there are four possible sets that you could lose), but there is only one way to win all four, and each of these five situations occurs with probability 0.5⁴ = 0.0625, because we have assumed that the result of each set is just a 50-50 shot. The probability of winning a match if you lose the first set is therefore 5 × 0.0625 = 0.3125 or 31.25%. Since the players are interchangeable, the probability of winning a match if you lose the first set must be the same as the probability that your opponent wins in the situation considered above. In other words, this probability is 1 − 0.3125 = 0.6875 or 68.75%. in this case, you are 2.2 times more likely to win a match if you win the first set than if you lose it. The result of a particular set, independent of all other results, affects your probability of victory by a difference of 0.375, or 37.5 percentage points.

Using the difference between the victory probability given that the first set is won and the victory probability given that the first set is lost as a measure of the value of a set, we see that, in this scenario, an individual set is worth more in the women’s game (0.5) than in the men’s (0.375). This is what we would have expected, since one set takes you half way towards your goal in a three set match, but only a third of the way in a five set match.

CONSIDERING THE QUALITY OF THE PLAYERS

Let’s look now at how these differences are affected when we change the value of P, the probability that Player A will win any particular set. Calculating the probabilities of victory in the women’s and men’s games, given that a first set is either won or lost, is a question of applying a particular statistical tool called the binomial distribution. This distribution tells us the probability of obtaining a particular number of ‘successes’ in a certain number of independent ‘trials’ (sets, in our case) where the probability of success in each trial is constant. Happily, this is exactly what we are looking for.

The probabilities for various values of P and the differences in victory probability in each scenario are collected in the following table:

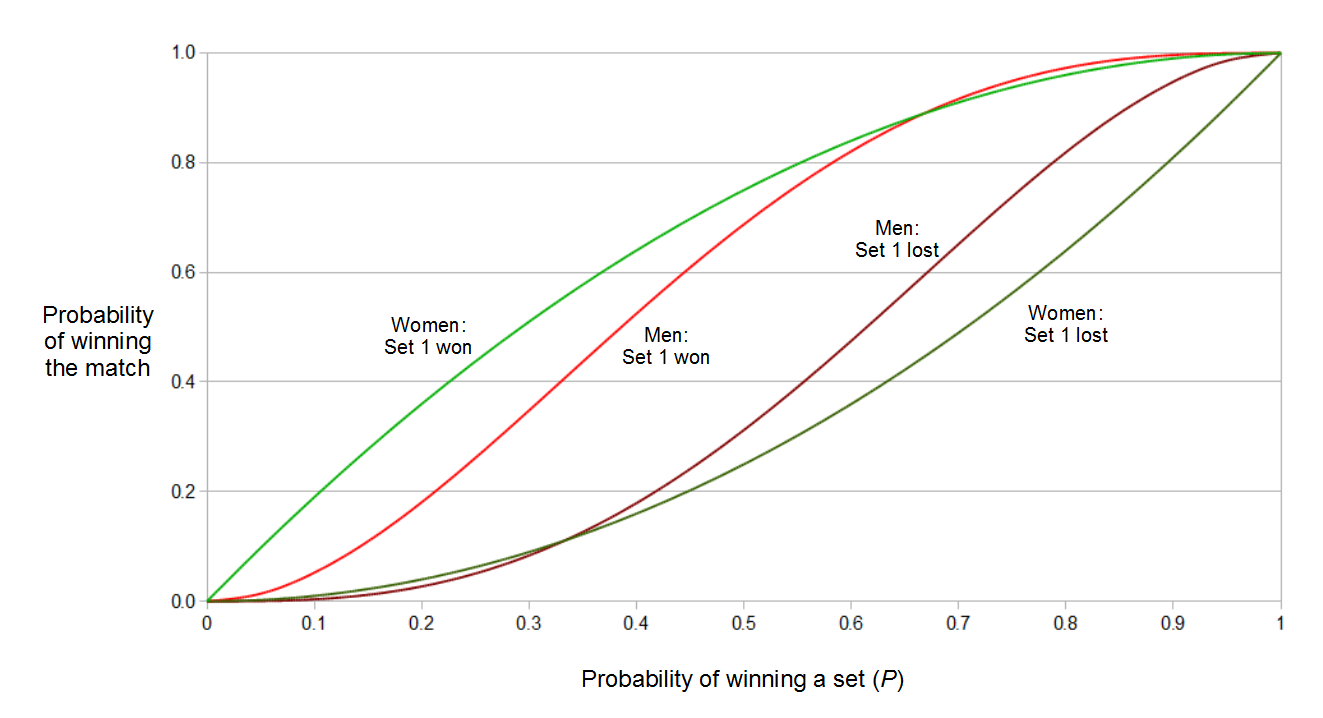
We can also show the various probabilities in a graph:

We see that winning the first set (represented by the brighter lines in the graph) generally results in a significantly higher chance of victory in the three-set women’s game than in the five-set men’s game, except for players who are significantly better than their opponents (P > 2/3), where the probability of victory for men is actually marginally above that of the women. Also, since the vertical distance between the green lines is always greater than the distance between the red lines, we see that the result of a set is always more significant in the women’s game than in the men’s game, no matter what the relative ability of the players happens to be.

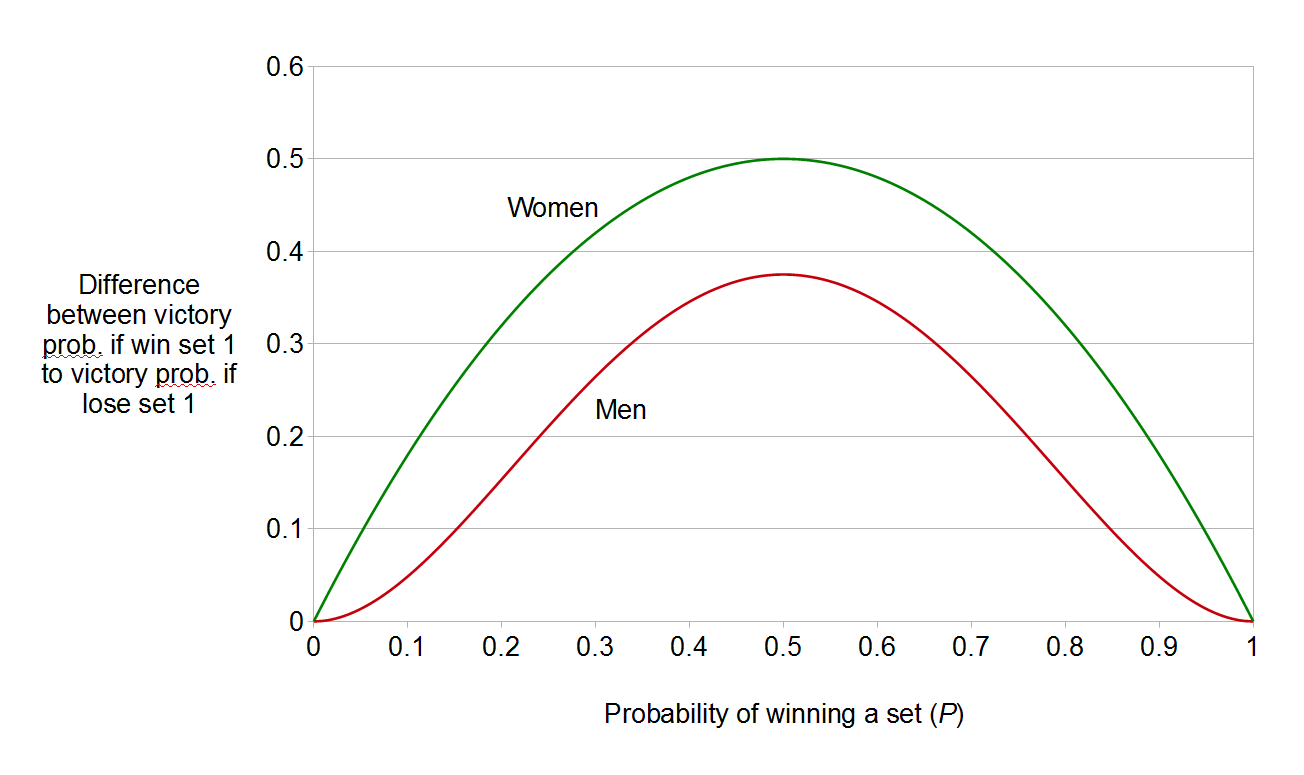
This is confirmed by looking at the graph of the victory probability difference measure that we have discussed:

So, if we are using the difference between the probability of victory after winning the first set and the probability of victory after losing the first set as a measure of the value of a set to each player, we may conclude that a single set is always more valuable in the women’s game than in the men’s (by a fairly consistent margin of between 12 and 20 percentage points, except in highly unbalanced matches), and, more strikingly, that sets are most valuable in very even matches, where the probabilities that each player will win a set are close to 0.5.

This is a conclusion that chimes with common sense. For a player who is much weaker than their opponent, snatching a single set against the odds is not necessarily a very significant event, because the other player remains very likely to reassert their superiority over the course of the remaining sets, particularly in the longer men’s game. Similarly, for a player who is a heavy favourite, winning a single set is not necessarily all that significant, because they were already very likely to win the match and their superiority makes it likely that they would have been able to mount a successful comeback from a one-set deficit anyway. On the other hand, in a very close contest an individual set can have a particularly significant effect on the final result, because the outcome of the match is so uncertain.

UPSETS: DO THE FACTS FIT THE MATHS?

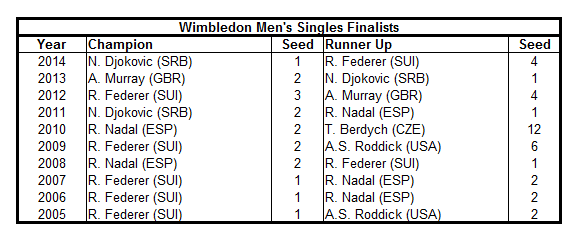
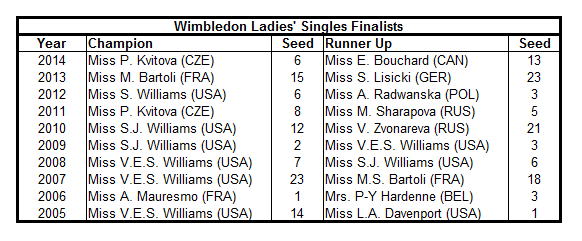
This simple analysis has confirmed that individual sets are more significant in the women’s game than in the men’s game. This means that we would perhaps expect to see more upsets in the women’s game, since, for a top player, the risk when losing a set is considerably greater. A quick look at the last ten years of Wimbledon finalists (surprisingly, the only Grand Slam for which I could find such a list that included the player seedings: Men here, Women here) would seem to support this conclusion. While the average seeding of the men’s finalists was 2.6 over this period, the average seeding of the women’s finalists was 9.5, suggesting a greater frequency of upsets in the women’s draw:

However, this is far from the whole story, because this higher rate of upsets in the women’s game appears to be a fairly recent development. Using only the seedings of Wimbledon finalists (admittedly a very crude approach), there appears to have been a sea change in women’s tennis in 2004. That year, the tournament was won by 13th seed, Maria Sharapova, but in the previous 36 years of open era tennis, 33 winners were drawn from the top three seed (the other three were seeded 4, 4 and 5), and there was only one finalist from outside the top eight  (Nathalie Tauziat, in 1998, seeded 16). The average seeding of women’s finalists in the period 1968-2004 was 2.77, lower than the figure for the men’s competition, which actually saw a number of unseeded finalists in that period.

Without investigating this in any great detail, there are a couple of reasons why the women’s game over this period may not have exhibited the higher rate of upsets that would be suggested by the mathematics, and which has been seen in more recent years. Firstly, the speed of serves in the women’s game has increased a great deal in recent times. The slower serving of previous years means a decreased advantage to the serving player, which reduces the levelling effect of serve alternation and emphasises the way that the scoring system in tennis multiplies up advantage, as we discussed earlier. This favours stronger players and would reduce the rate of upsets.

Secondly, the global spread of women’s tennis seems to have accelerated since the turn of the millennium, with debut Grand Slam titles for players of six new nationalities since 2003, including Russian players (now a major force in the sport) and the Chinese player Li Na, heralding a potential new era for the popularity of women’s tennis in Asia. This suggests that the pool of players in previous years was probably considerably smaller than it is today, which would mean a more rapid drop-off in ability as you move down the rankings, which once again would favour stronger players and reduce the rate of upsets.

MATCH POINT

So, what have we concluded from all of this? Basically, sets are more valuable in the women’s game than in the men’s; winning or losing the first set generally affects your chance of victory by around 15 percentage points more in a three-set match than in a five set match. The exception is matches in which one player is heavily favoured (with a greater than 90% chance of winning each set), where the difference becomes less important.

Also, sets are most valuable in close matches. In a perfectly balanced match, the result of a single set can affect your chance of victory by 50 percentage points in the women’s game (75% chance of victory if you win the first set, versus a 25% chance if you lose it) and 37.5 percentage points in the men’s game (68.75% versus 31.25%). However, if there is a genuine mismatch between the players, the result of the first set will have a limited impact on the likely result of the match, particularly in the longer men’s game, where superior skill has a greater opportunity to exert itself.

---

Thomas Oléron Evans, 2015

---

* At the most prestigious tournaments at any rate.

** These are the figures for the Australian Open, the French Open and Wimbledon, where tiebreakers cannot be played in the final set. At the US Open, where tiebreakers may be played to decide any set, these percentages are marginally lower.

*** There is a slight mistake in the final answer given at the linked page, but the working is all correct.

**** I say “theoretically”, because the computing power required to evaluate any particular chess position precisely is generally prohibitively enormous. xkcd has a nice post on the “difficulty of various games for computers”.

---

IMAGES
Serena Williams – Wikimedia Commons, CC, Yann Caradec
Andy Murray – Wikimedia Commons, CC, Carine06
Maria Sharapova – Wikimedia Commons, CC, Charlie Cowins
Novak Djokovic – Wikimedia Commons, CC, Christopher Johnson