SOLUTION
There is only one solution. This one:
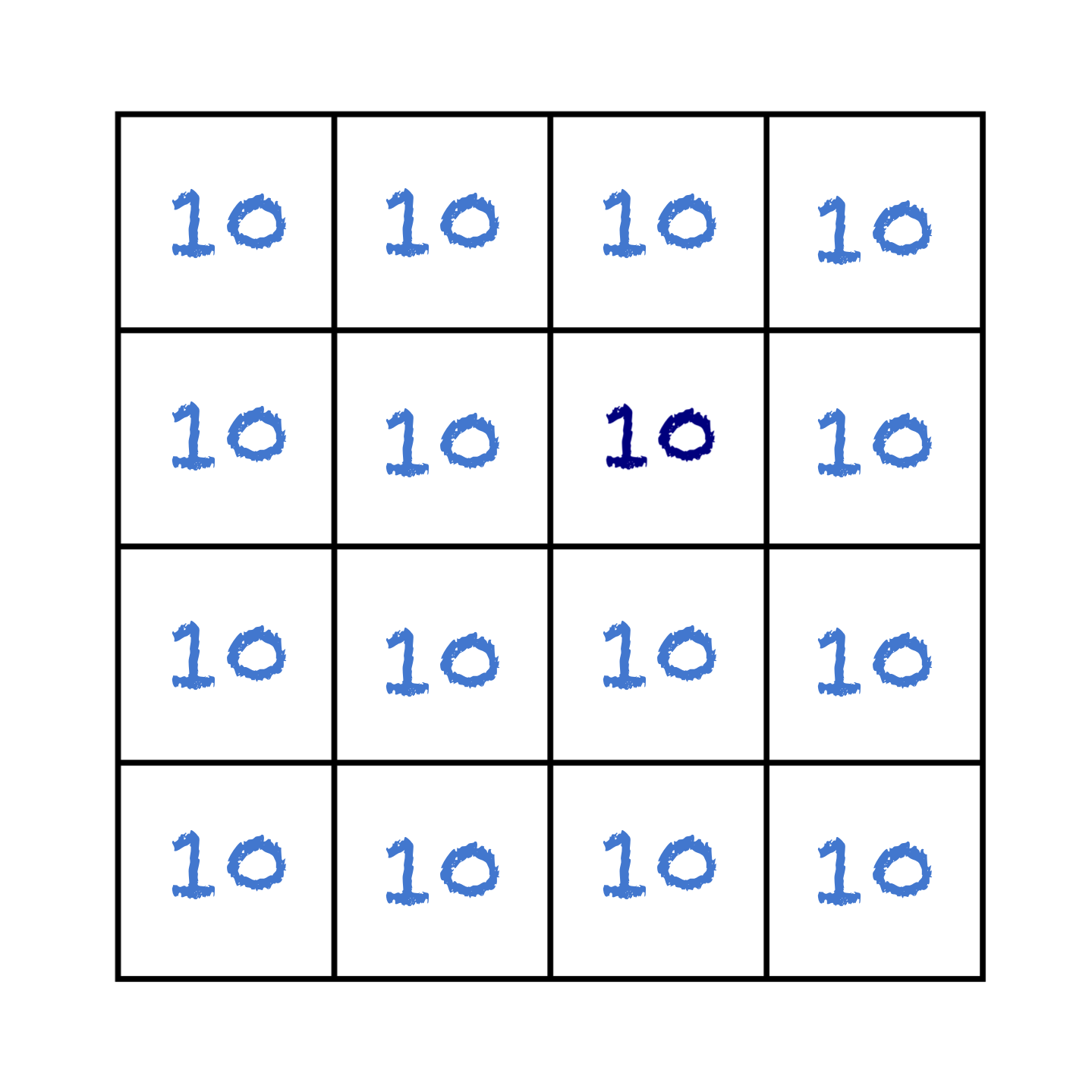 .
.
WHY CAN’T THERE BE ANY OTHER SOLUTIONS?
There is a very neat proof that this is the only solution.*
Suppose we have found a different solution from the one given above. Now, no matter how we have completed the grid, somewhere on it there must be a minimum value. Possibly that minimum value appears more than once, but there must be at least one cell that we can point to and say “No other numbers in the grid are smaller than this one.” Let’s call that minimum value m.
Since we know that not every value in our grid is the same (that would give us the solution pictured above, but we have a different solution), somewhere on the grid there must be a cell containing the value m which is adjacent to a cell containing some other larger value. So, we have a cell containing the value m, with a neighbour containing a value larger than m, and no neighbours containing values smaller than m (because m is the minimum)… so that cell cannot possibly be the mean of its neighbours. Our “different solution” is not a solution at all.
In other words, there are no different solutions. The solution pictured above is the only one.
In fact, by the same argument, no matter what kind of grid we had been given – perhaps a hexagonal grid, a three-dimensional lattice of cubes or something completely irregular – provided that all the cells are connected, the only possible solution would be to write the same number in every box.
SOME THOUGHTS ON USING THIS PUZZLE WITH STUDENTS
There are a few nice learning points to draw out of this puzzle:
- All tens? Isn’t that cheating?
.
This is something I have often heard from students (and even from some teachers) when confronted with this puzzle. There is an assumption that filling every cell with the same number is somehow cheating. This is a good opportunity to highlight the importance of not making assumptions and of using (and understanding) mathematical language in a precise way. If the question does not say something is not allowed, then it cannot be cheating!
. - Focus on the extremes.
.
The puzzle highlights a fundamental principle of problem solving: If in doubt, focus on the extremes. Extreme points are often where you learn most about how things work or why rules might break down. Think about the biggest or smallest values; think about the corners or the endpoints; look for what happens at zero or as you head towards infinity… Often, as in this puzzle, if you think about the extremes, everything can become clear.
- You don’t need any examples to prove something.
..
The proof given above is really just one simple idea: the minimum value cannot possibly be the mean of its neighbours. It is an intuitive example of a proof by contradiction. The fact that you can show that something is true through the sheer power of your imagination and your logical reasoning – simply by asking yourself “What would a solution look like?” – with no need for messing around with actual numbers, is an amazingly powerful idea.
.
Moving from performing calculations to proving results can be a difficult conceptual leap, but it is an essential one for students who want to take Maths beyond A-level. I also believe that the ability to apply logic to make rational objective deductions is a valuable skill more generally, whether or not you want to study Maths. Simple logical arguments like this one can provide a route into the necessary ways of thinking to allow students to gain this skill.
.
Click HERE to return to the Puzzles page.
* There is also a very ugly proof, which involves writing down sixteen linear equations in fifteen variables and solving them simultaneously. For those tempted to to that, I would invite them to solve the same problem on a 1000 × 1000 × 1000 × 1000 four-dimensional hypercubical lattice. That should dampen their enthusiasm for linear algebra.
