Near misses:
Thanks to all those who had a go at this. It was great to see people enjoying wrestling with the logic of the puzzle. A variety of valiant yet unsuccessful attempts were proposed until one Twitter-user eventually came up with not one but two correct solutions.
Here is a good early proposal from @GHSMaths:
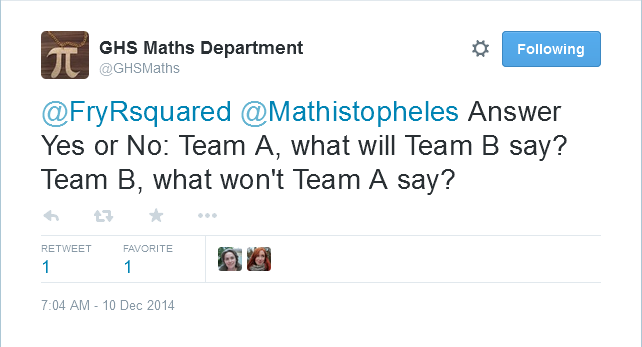This suggestion would be a correct answer, were it not for the fact that I specified that the same question should be asked of both teams. Some people tried to get around this by linking the two questions into a single sentence, using a structure like “If you’re A then XXXXX, but if you’re B then YYYYY?” However, this is still two questions.
(Also, on a point of extreme pedantry, as someone pointed out, GHS Maths’ proposal might technically be described as a “Yes”/”No” question rather than a Yes/No question. Yes and No are not being used meaningfully here and could equally be replaced by Dog/Fish or whatever. This is one thing that I was trying to avoid by stating that Yes and No should be “grammatically sensible answers”, though I admit that this phrase does not really convey this successfully.)
In any case, the answer was on the right lines.
This solution from Troy R is also worthy of comment for the sheer amount of mental effort that it would demand of the poor teams.
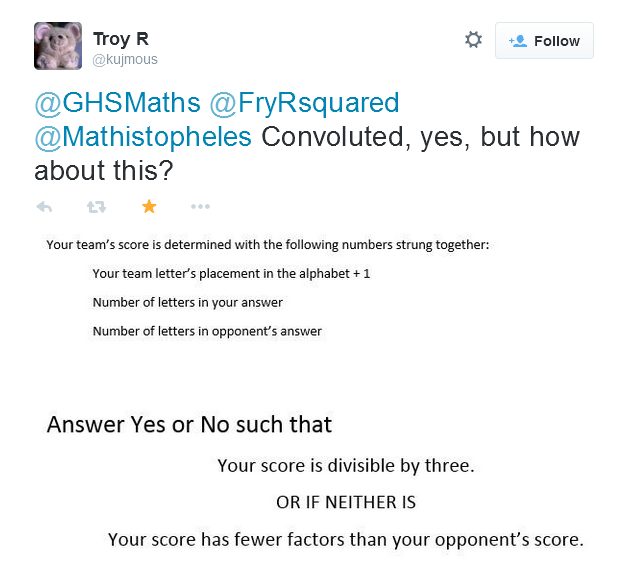Unfortunately, it turns out that the logic of this idea doesn’t quite work out, because one player can force a win with their choice of answer. It also doesn’t really count as a question, but again, it was on the right lines in its simultaneous consideration of both team names and answers.
Solution:
Although it is dressed up differently, the approach required for this puzzle is similar to that used in puzzles of the “One of them always lies, one of them always tells the truth” variety. Incidentally, for those who enjoy such puzzles, here is a fantastic book which takes you through every conceivable (and inconceivable) permutation.
To approach our problem, we first observe that who wins and who loses can clearly only depend on the answers that the teams give to the question that you ask them. Since it must be a Yes/No question, there are only four possible outcomes: YY, YN, NY, NN, and each of these must correspond to a win for A (and a loss for B) or a win for B (and a loss for A), since we require that the question will definitely separate the teams.
Suppose that both outcomes in which A answers Yes (YY and YN) corresponded to a win for A. This would mean that A could guarantee victory by answering Yes, which is not allowed. Following this logic through, we find that YY and NN must correspond to a win for A, while YN and NY must correspond to a win for B, or vice versa.
Next, suppose that the text of the question does not refer to the answer given by the opposing team. This is impossible, since, the scenarios YY and YN, which must be marked differently for A, could not then be distinguished.
Furthermore, suppose that the text of the question does not refer specifically to the names of (at least one of) the teams. This is also impossible, since, in this case, the teams would be indistinguishable and YN could not be marked incorrect for A, while NY was marked correct for B (or vice versa), as is required.
Therefore, we are looking for a question which refers to the opponent’s answer, which refers to at least one team by name and which marks situations in which both answers are the same as correct for Team A and incorrect for Team B, while marking situations in which both answers are different as correct for Team B and incorrect for Team A (or vice versa).
The question that I had in mind was:
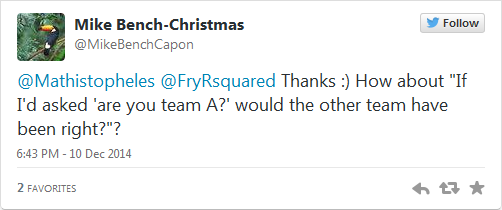
‘If I had asked the question “Are you Team A?”, would the other team’s answer be marked as correct?’
Hearty congratulations to Mike Bench-Capon who came up with this exact question and even managed to fit it into a tweet:
In fact, Mike had already submitted a different correct answer, which exploited the lexical properties of the letters A and B and the words “Yes” and “No”:
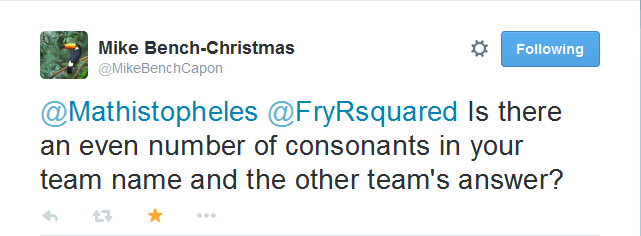Although this question has certain disadvantages in relation to the previous one, since it would not be elegantly generalisable to all possible pairs of team names (or to other languages), if you work the logic through, you will find that it is indeed a correct answer, and a pretty clever one at that.
Thomas Oléron Evans, 2014
This does not solve the riddle, does it?
Unless it is a trick of linguistics: “marked as correct”, vs. “True” vs. “affirmatively marked”
‘If I had asked the question “Are you Team A?”, would the other team’s answer be marked as correct?’
1. Who is marking it as correct?
2. What does “correct” mean? That they are telling the truth, or that they are giving an affirmative answer to the question “Are you team A?”
i.e.
In answer to your tie-breaking question:
Team A logically assumes that team B, when answering that question, would say “No”. Team B’s answer would be correct (that they are not team A), so team A’s answer is “Yes” (That Team B’s answer is correct.)
Team B logically assumes that team A, when answering that question, would say “Yes”, their answer would be correct, so team B’s answer is “Yes” (Team A’s answer is correct.)
As long as they say yes, they are right. No tie broken.
But perhaps I am missing some logic here or the rules of pub quiz.
My wording is intended to mean “Would the answer that the other team provides to THIS QUESTION (i.e. the “Yes” or “No” that they write down NOW) be the correct answer FOR THAT TEAM if the question had not been this one, but had actually been ‘Are you Team A?’?”
If both teams answer “Yes”, then Team A’s answer would be a correct answer to ‘Are you Team A?’ and Team B’s answer would be an incorrect answer to the same question. Therefore, in writing “Yes”, Team A is INCORRECT, since they are asserting that Team B’s answer would be a correct answer to the question ‘Are you Team A?’, and we have just established that this is not the case. Similarly, in writing “Yes”, Team B is CORRECT, since they are asserting that Team A’s answer would be a correct answer to the question ‘Are you Team A?’, which is indeed the case.
Similar logic demonstrates that Team B is correct if and only if the answers are the same while Team A is correct if and only if the answers are different.
Yes but team b wld answer no and team a yes they will not both answer yes right?
The question is:
‘If I had asked the question “Are you Team A?”, would the other team’s answer be marked as correct?’
If Team B writes “No” then they are asserting that the other team’s answer would NOT have been marked as correct if the question asked had been “Are you Team A?” However, you say that Team A’s answer is “Yes”, which clearly WOULD be correct (for that team). Therefore Team B has answered incorrectly in the scenario that you put forward.
You can work through similar logic to see that Team A’s answer is correct. If either team were to answer differently, the situation would be reversed and Team B’s answer would be correct, Team A’s would be incorrect. However, if both were to answer differently, the situation would remain as above, with Team A prevailing.