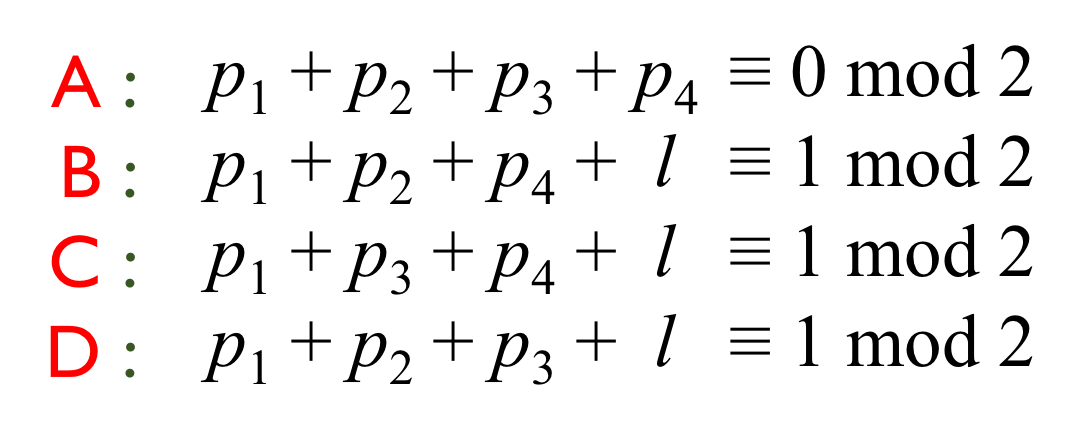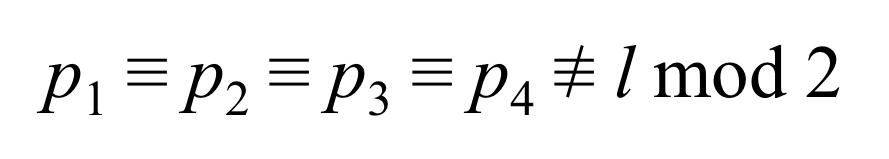Happy Boxing Day!
Throughout the month, to accompany the release of our book on the Mathematics of Christmas, Hannah Fry & I were tweeting out Christmathsy bits and pieces, one a day, advent calendar style.
A final post, to provide the solution to Friday’s puzzle.
CLICK HERE TO SEE THE WHOLE CALENDAR
SOLUTION TO FRIDAY’S PUZZLE
Click here for Friday’s puzzle.
Scroll down for the solution…
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Solution to Day 23
Part One – Merry
Example optimal solution:
ABDABDCBDA (10 rooms)
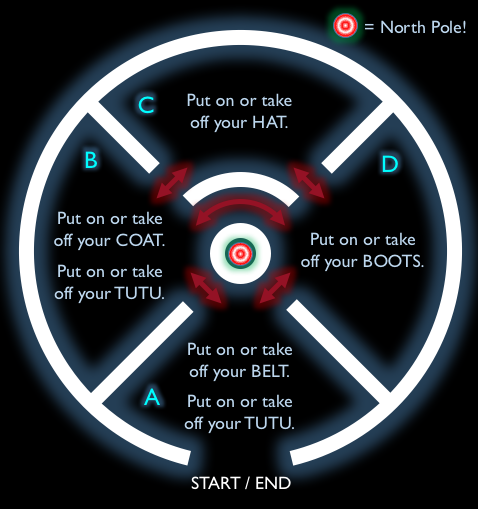The first thing to notice is that Santa must visit each room an odd number of times, since each contains a unique item that he must put on (and he removes the item on every second visit). Helpfully, this means that the tutu is irrelevant to the puzzle; since Santa must visit each of A and B (where the tutu is mentioned) an odd number of times, his combined number of visits to these rooms must be even, whether or not the tutu is considered. We can therefore forget about it and concentrate on the other items.
Now, thinking in terms of individual rooms is not very helpful, since Santa is not free to visit them as he chooses. He cannot decide to complete a path involving 5 visits to A, 7 to B and 1 each to C and D, say, because such a path is not possible. What we need to do is break down all his possible paths into their most fundamental components.
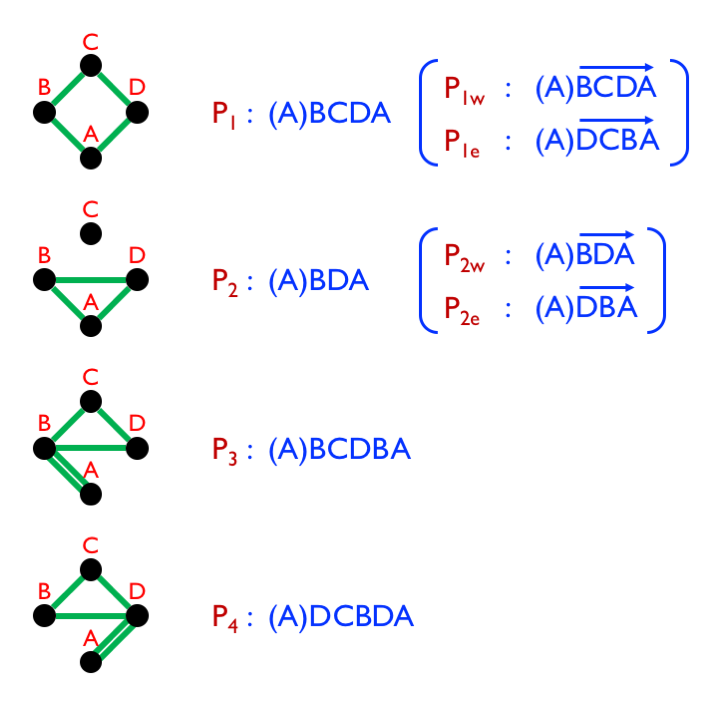
Specifically, each time Santa leaves A, there are only four basic routes he can take to get back:
The first A is bracketed in each case, since it is considered as a starting point for each path, rather than as a room visited on the path itself.
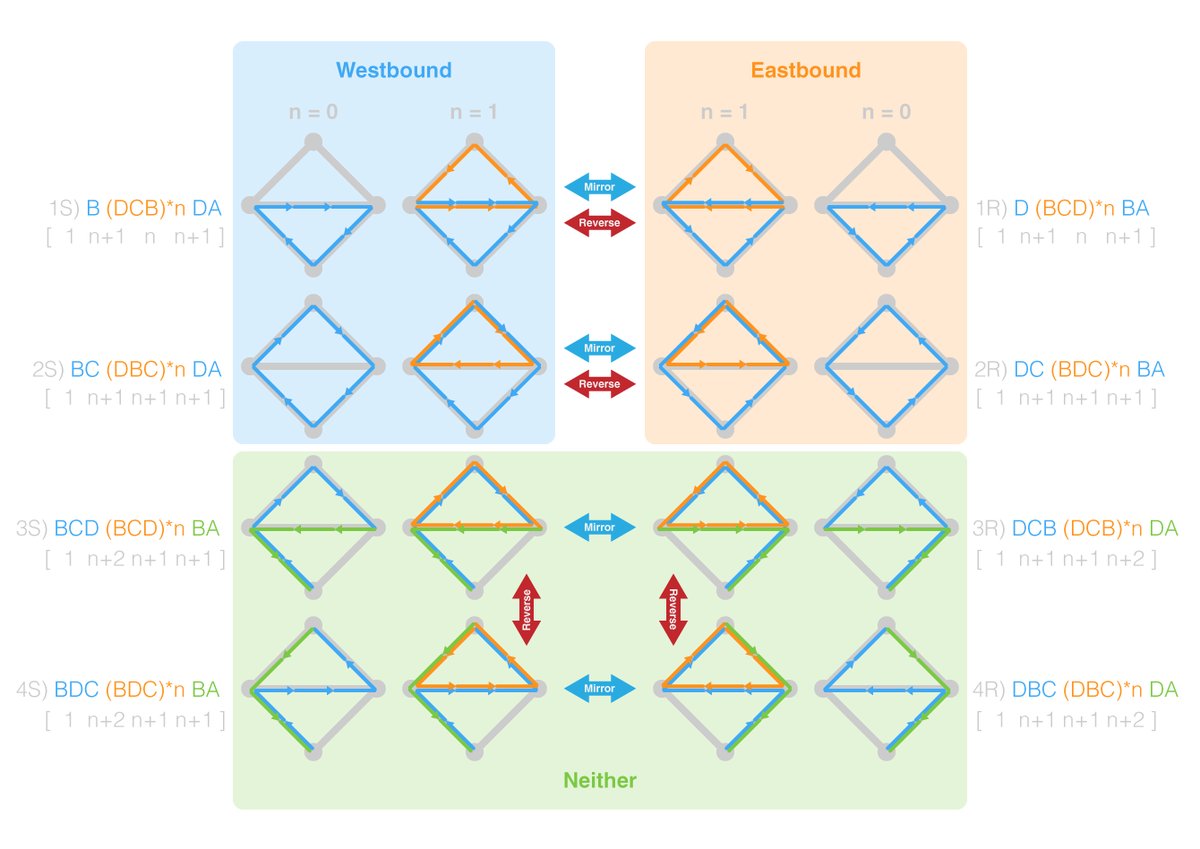
Note that P1 and P2 each have a Westward and an Eastward variant, but we won’t need to consider these until the second part of the puzzle. Although P3 and P4 can also be followed in two different directions, these are completely interchangeable for the purposes of both puzzles, so the distinction can be ignored.
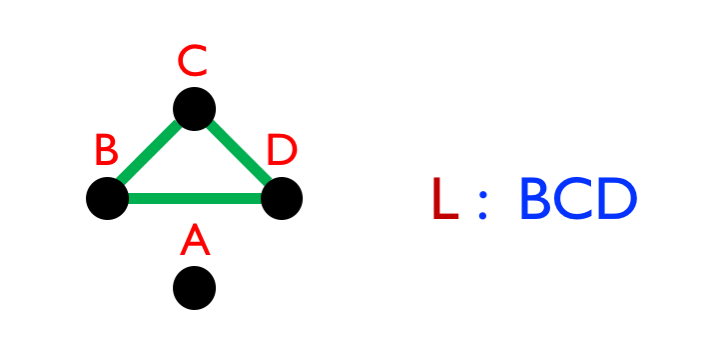
Now, you may feel that there are other possible paths that can be taken to return to A: (A)BCDBCDA, for example, or (A)DCBDCBDCBDA. However, it is actually clear that any such path is just a combination of one of the four basic paths with a certain number of tours round the following loop:
If Santa starts at A, then, these five elements – P1 to P4 and L – can be combined to create every possible path that he could take through the changing rooms. Furthermore, almost* any combination of the elements corresponds to a possible path, or to many equivalent paths, depending on the order and direction in which the components are put together.
For example, the combination P1P1P4LL (colours for illustrative purposes only) corresponds to several paths – including ADCBADCBADCBDCBDCBDA and ADBCDABCDBCDABCDBCDA – all of which are equivalent for the purposes of the first puzzle, since they pass each room the same number of times (4A,5B,5C,6D, in this case).
The next step is to determine how many times each component must feature in a possible solution. If we let lower case letters represent the number of times each component is included in a path, we can use the fact that each room must be passed an odd number of times (though, since A is the starting point, it must actually feature in the components an even number of times) to create the following equations:
If two things are congruent (≡) mod 2 it simply means that their even/odd status is the same, so “≡ 0 mod 2” means the left hand side of the equation is even, while “≡ 1 mod 2” means the left hand side is odd. Taking the equation for D as an example, D features once in P1, P2, P3 and L (its two appearances in P4 cancel out), and it must be visited an odd number of times, so the sum of the number of times that each of these components is used must be congruent to 1 mod 2.
Now, the four equations can be solved simultaneously to give the following relationship:
In other words, there are two families of solutions to the puzzle**:
- P1 to P4 are each included an even number of times,
L is included an odd number of times; - P1 to P4 are each included an odd number of times,
L is included an even number of times
From the point of view of finding the shortest path, the first option is clearly better, since it allows three of the components P1 to P4 to be omitted (zero being an even number), implying that the optimum solution for the first puzzle must be of the form P2P2L (since P2 is the shortest of P1 to P4, of which at least one must be included), giving solutions like ABDABDCBDA, of length 10.
Part Two – Mayhem
Example optimal solution:
ABDABCDBADCBADCBDA (18 rooms)
Firstly, any solution to the harder puzzle must also be a solution to the simpler puzzle, so the two families of solutions identified earlier are still relevant. However, Santa now also needs to ensure that he completes an odd number of Eastward circuits (P1e & P2e) and an odd number of Westward circuits (P1w & P2w).
The key observation here is that, in order to do this, Santa needs to reverse his direction of travel around the pole and the only components that allow him to do this are P3 and P4. However, in the first family of solutions, these components must be included an even number of times. What is more, if Santa follows P3, he cannot follow P3 again until he has followed P4 (since he would otherwise be heading in the wrong direction), so if one of these components is included twice, the other must also be included twice.
All of this means that a solution of minimum length from the first family of solutions would be of the form P2eP2wP3P3P4P4L (an extension of our earlier solution to include P3 and P4), such as ABCDBADCBDABCDBADBADCBDABDCBDA, of length 30. However, a solution of minimum length from the second family – in which P1 to P4 are included once each (with one of P1 and P2 in its Eastward form and the other in its Westward form) and L is omitted – is considerably shorter: P1eP2wP3P4 corresponds to solutions such as ABDABCDBADCBADCBDA, of length 18.
Congratulations
Congratulations first of all to NickTR and Catherine Evans*** for solving the first puzzle, and to Olaf Doschke for finding the optimal solution and providing these insightful comments:
There were also four people who really went above and beyond with this one.
Firstly, Troy ToTheWorld who found optimal solutions for both puzzles and wrote a program to exhaustively search all possible paths of a certain length, which is apparently still working on verifying the optimality of his second solution.
Secondly, Juan Pedro Fisanotti, who also found optimal solutions for both puzzles and verified their optimality using a great python program that he has made available online.
Thirdly, Stephen Morris found optimal solutions for both puzzles and presented a cunning proof of their optimality via the comments:
Finally, though, we have RepliCat, who not only found optimal solutions, but also produced this beautiful image detailing all the possible subpaths and used it to prove analytically that these solutions were the optimal:
Well done to all! As a reward, you each get a second Christmas on the 29th December. Perhaps you could all celebrate it together. Be sure to send some photos.
* The exceptions are, trivially, combinations like LLL, which involve only L, and, less trivially, combinations like P1P2P3P3P3P4LL, in which the difference between the number of P3 and P4 elements is greater than 1. Combinations of the second type do not form paths since Santa is not allowed to enter and leave A through the same doorway.
** The fact that we have not found a unique solution was to be expected, since we had more unknowns (5) than equations (4).
*** Thanks, Mum.