Happy 22nd of December!

Throughout the month, to accompany the release of our book on the Mathematics of Christmas, Hannah Fry & I are tweeting out Christmathsy bits and pieces, one a day, advent calendar style. Assuming we don’t run out of ideas, that is…

You may remember from Day 10 that Santa is not all that good with passwords and security. Well…

Here’s the letter in copyable form:

05-06-02-19 20-02-15-21-02. 17-13-06-02-20-06 04-16-22-13-05 26-16-22 03-19-10-15-08 14-06 02 ~**MESSAGE~CORRUPTED**~ 6765-10946-8-233-233-1-10946-8-5 55-3-987-6765-1-34-8-5-4181-987-610. 10946-34-1-610-144 121393-987-17711. 1-1-4181-1 (1-21-8-5 8)

Answers via the comments or on Twitter. All correct answers will be rewarded with deep respect and warm Christmas wishes. Enjoy!

CLICK HERE TO SEE THE WHOLE CALENDAR SO FAR

---

SOLUTION TO YESTERDAY’S PUZZLE

Click here for the puzzle.

Scroll down for the solution…

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

Solution:

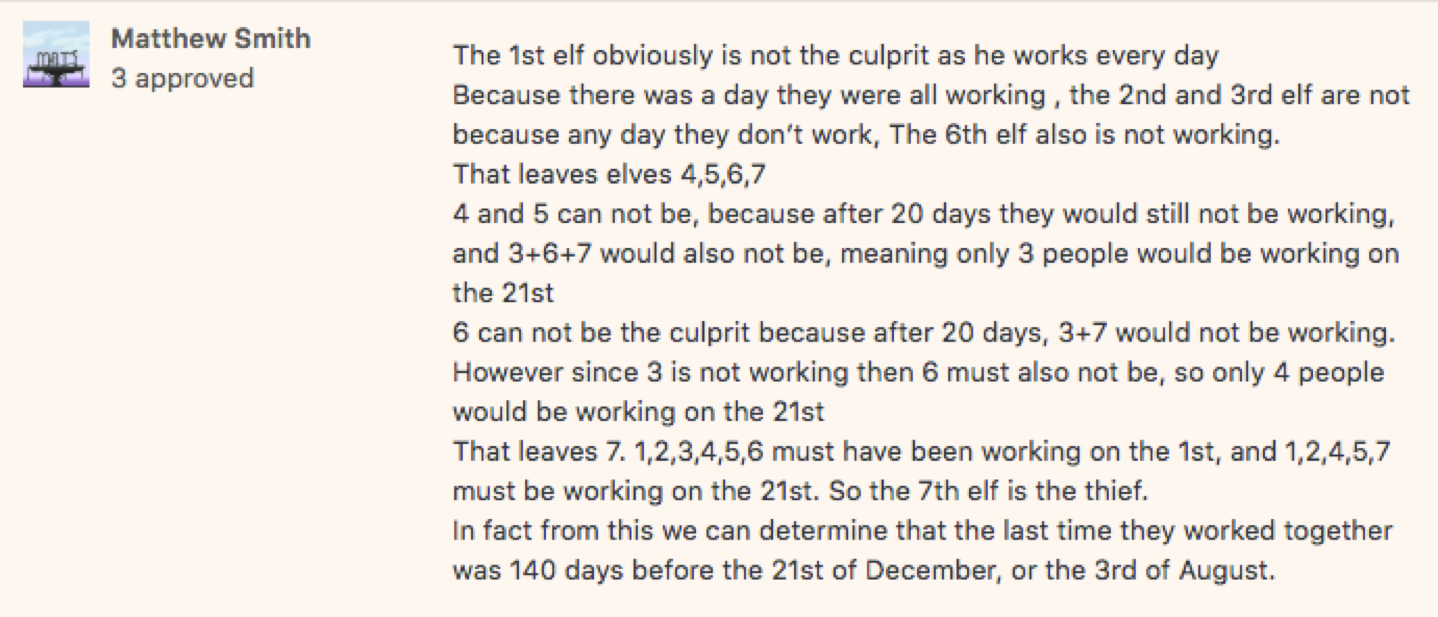
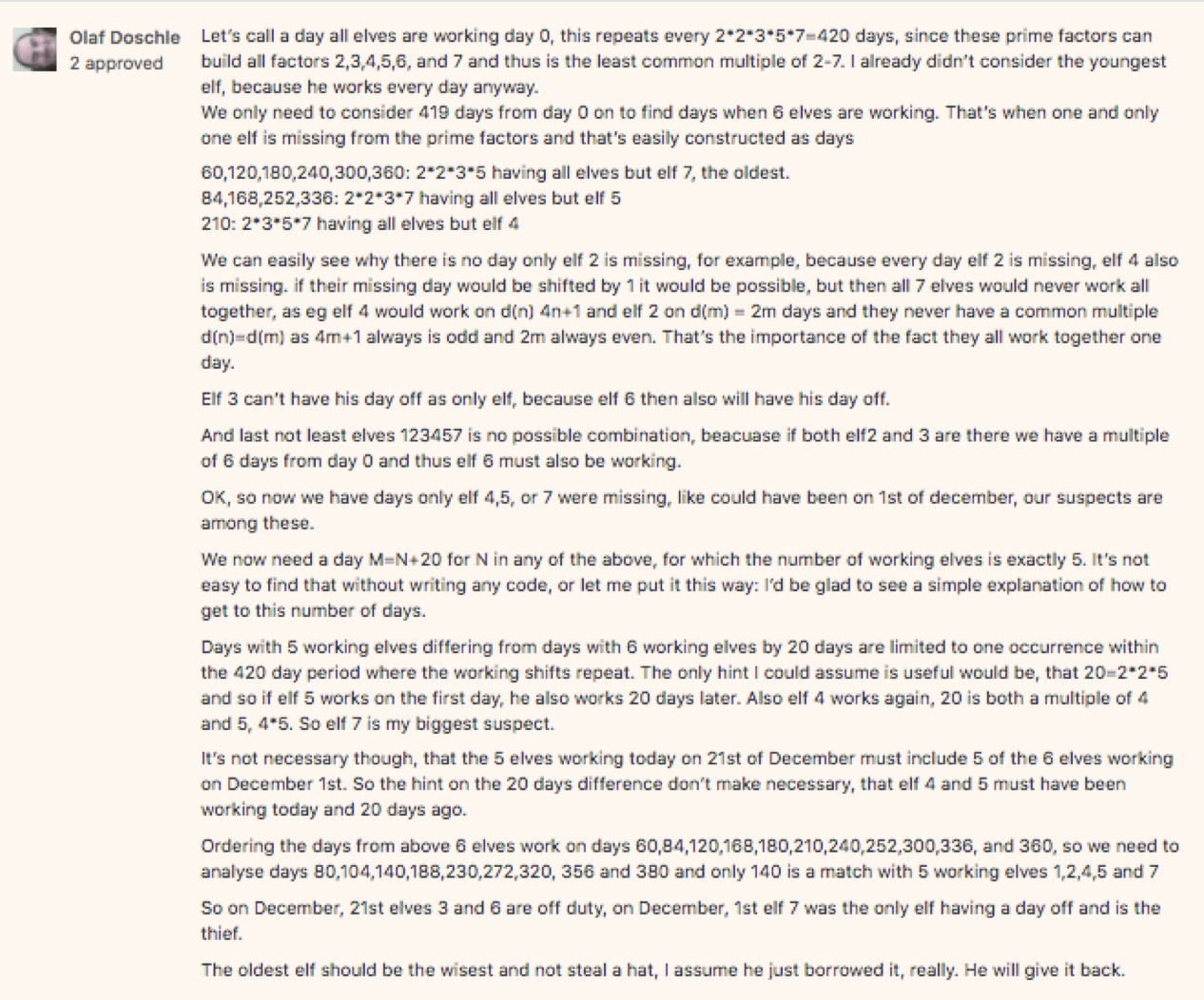
We know that all 7 elves (let’s call them E1 to E7, in increasing order of age) were working together on some day, so let’s call that Day 0 and number all subsequent days accordingly. We also know that 6 elves were working on 1st December, so just 1 elf was missing.

Now, the missing elf can’t be E1 (who works every day). It also can’t be E2, since that would mean that 1st December was an odd numbered day, so E4 and E6 would not be working either. Nor can it be E3, since that would imply that 1st December was not a ‘multiple of 3’ day, so again E6 would not be working. Finally, the missing elf can’t be E6, since that would imply that 1st December was not a ‘multiple of 6’ day, so at least one of E2 and E3 would not be working. So the missing elf was E4, E5 or E7.

We now know that E1, E2, E3 and E6 were working on 1st December, and 20 days have passed since then, so E1 and E2 must also be working today (since 1 and 2 divide 20), while E3 and E6 must NOT be working (since 3 and 6 do not divide 20). Since there are 5 elves working today, that means that E4, E5 and E7 must all be working. But that means that E4 and E5 were also working on 1st December, 20 days ago (since 4 and 5 divide 20).

Therefore, E7, the oldest of the elves, is the only one who was not working on 1st December. So the oldest elf is the thief!

Brilliant response to this puzzle again, with some serious effort going into the solutions. Along with explanations of the logical reasoning (see below), there were spreadsheet based solutions (Kostas Cheliotis, Gareth Adams, Chris Emerson), a worked number theory solution (Shawn Chapla) and a programming solution (Eoin Travers).

Here are some explanations of the solution from Matthew Smith, Olaf Doschke, ExceptionalLiar and Ben Tomkins (I particularly like Olaf’s closing paragraph, though if the oldest elf is only allowed to earn 14% of a full time salary, commensurate with his or her working hours, you can understand why thieving may seem like the only option):

Other correct solutions came in from Troy ToTheWorld, Fergus Johnson and Catherine Evans.

Congratulations to all on your promotion to Interpol’s new North Pole division.