This post is about the mathematically perfect way to organise your office Secret Santa, as discussed in a new book that I have written with Dr Hannah Fry: “The Indisputable Existence of Santa Claus: The Mathematics of Christmas”.
Here’s the problem, in its full mathematical glory.
To completely fulfil our secrecy condition, once you know who you are buying for, that person must be equally as likely to be buying for you as anyone else is. In other words, if the number of participants in your Secret Santa is n, the probability that you are your Secret Santa’s Secret Santa should be 1/(n–1); you have n–1 possible Secret Santas and all must be equally likely.
However, as we have seen, in our proposed system, with at least three participants, that probability is actually zero. There is no chance that your giftee is also your gifter.
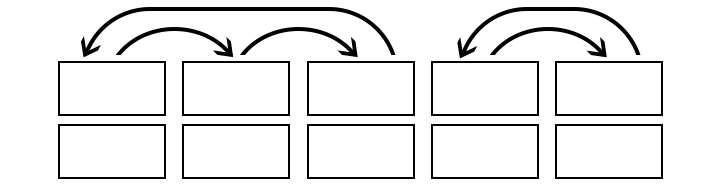
So here’s an alternative system. Everything is the same as before, to begin with. You make the same cards, shuffle them up, lay them out in a row, cut them in half… But this time, rather than shifting the top half of every card one place to the right, you do something slightly different:
Exchange the top halves of the final two cards, then treat the other cards exactly as you did before. Shift each top one space to the right until you come to the final card before the two you’ve already switched, then put the top of that card back to the start. Finally, stick the new tops and bottoms together again.
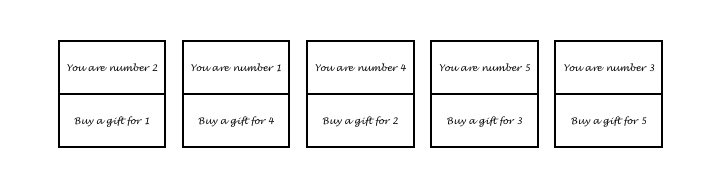
As before, you mustn’t look at these cards, but they might now look something like this:
With this system, the last two cards show two people buying for each other, which is what we want. The only problem is that the probabilities don’t work.
We want the probability of being your Secret Santa’s Secret Santa to be 1/(n–1), but if you draw one of these cards at random the chance of this happening is actually 2/n*; two of the n cards available are part of that pair of mutual buyers. That means that, using this system, the chance that the person you’re buying for is also your Secret Santa will be roughly double the chance that any other person is buying for you.
So our original system (let’s call it System Santa) gave us too little probability of being our Secret Santa’s Secret Santa, while our new system (System Rudolph) gives us too much. What we need is some combination of the two. If there was just the right level of uncertainty over which system we were using, we could get to that 1/(n–1) probability that we’re after.
How much uncertainty, though? Well, maths can give us the answer.
Suppose we use System Santa with probability p and System Rudolph with probability 1–p, as shown in this chart:
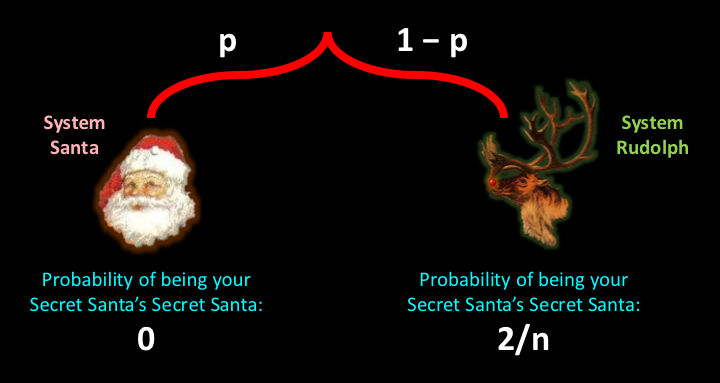
Since you can only be your Secret Santa’s Secret Santa under System Rudolph, the probability of this happening is now (1–p)(2/n). We want this probability to be equal to 1/(n–1), so to find the probability p we just need to solve the equation:
1/(n–1) = (1–p)(2/n)
A bit of rearranging gives us the solution: p = (n–2)/(2n–2). In other words, there should be n–2 chances in 2n–2 of using System Santa and n chances in 2n–2 of using System Rudolph.
But remember, you can’t just work out which system to use by using a random number generator** or anything like that. That would still be a violation of the secrecy condition, because even you, the organiser, are not allowed to know which system is being used.
So here’s an actual solution. For each participant of your Secret Santa, make a complete set of cards using System Rudolph and put each set into a separate envelope. Then, for each participant of your Secret Santa but two, make a complete set of cards using System Santa and put each of those sets into a separate envelope as well. Every envelope must be identical. Then simply shuffle the envelopes, select one at random and use that set of cards for your Secret Santa.
Easy, hey?
The tiny drawback here, obviously, is that you have to make quite a lot of cards. For n participants, you need to make a fairly daunting n(2n–2) cards in total***, a number that grows quadratically with the number of participants. You will need:
- 40 cards for 5 participants;
- 420 cards for 15 participants;
… and a fairly eye-watering: - 1200 cards for 25 participants!
So if you really, really, really want to make your Secret Santa as perfect as perfect can be, and you don’t mind some serious blisters on your scissor fingers and a repetitive strain injury to nurture for the rest of your days, you go ahead.
We’re going to stick with our original system though…
* Assuming that there are at least five participants.
** For example, copying the text below into a cell in Excel (replacing n, with appropriate number of participants) will tell you which system to go with, following the correct probabilities:
=IF(RAND()<(n-2)/(2*n-2),”Santa”,”Rudolph”)
*** Actually, since n and n-2 have a common factor of 2 when n is even, you could get away with making only (n–2)/2 Santa sets and n/2 Rudolph sets, for a total of n(n–1) cards, thus halving your workload. There are no such short-cuts with an odd number of people though…
Thomas Oléron Evans, 2016