–
Happy 6th of December!
Throughout the month, to accompany the release of our book on the Mathematics of Christmas, Hannah Fry & I are tweeting out Christmathsy bits and pieces, one a day, advent calendar style. Assuming we don’t run out of ideas, that is…
Another puzzle today:
And take note of this observation from Michael Baym:


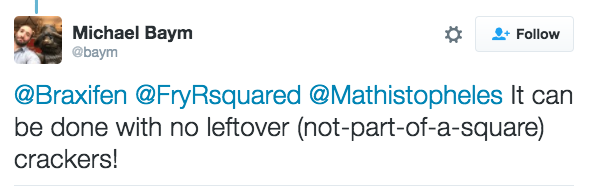
I can’t see how to do it with no leftover parts of a square. In the diagram, sixteen crackers are used. If the four squares aren’t split up, the maximum number of crackers that can be used is 13. If the four squares are split up three and one, the maximum number of crackers that can be used is 14, and this number is the same if the four squares are split up two and two. In this case, there will either be one more square or some pieces sticking.
Thanks for taking an interest in the puzzle! The answer is on Day 7 if you want to have a look: