Obviously, the tiles must not overlap one another and must not overlap the boundary of the blue square.
[UPDATE: See the bottom of this post for the answer to this question, provided by Stephen Morris.]
This question was inspired by a tweet from James Tanton:
Is it always possible to fit a set of squares with total area 1 within a square of area 1 with no overlap?
— James Tanton (@jamestanton) July 14, 2015
The answer to that question is “No”. Many combinations of squares with total area 1 do not work. For example, as Alex Schaefer replied:
James Tanton’s question got me thinking about other possibilities for square tiling problems, particularly the one at the top of this post. I am finding it frustrating, because I certainly feel like I know the answer, but I cannot see a simple proof.
Is the answer what I think it is? Is there an easy way to show it?
.
UPDATE:
Many thanks to Stephen Morris (one of the people behind The Math Factor podcast) for his detailed and meticulously researched response to this question. It turns out that the answer was indeed what I thought it was (the tiling is possible if and only if r is rational), but it seems that this is by no means obvious.
Here is Stephen’s response in full:
This puzzle made me think of Stan Wagon. He made his name as a young man with his ‘Fourteen Proofs’ paper in which he presented fourteen proofs of a similar tiling theorem. Like your problem it is easy to state but difficult to prove. Definitely worth a read! Maybe you can come up with some more proofs.
http://www.maa.org/programs/maa-awards/writing-awards/fourteen-proofs-of-a-result-about-tiling-a-rectangleStan told me that your problem was solved by Max Dehn in 1903. This is a fascinating field and I’ve enjoyed reading up on it over the last few days.
Your conjecture is that in a square tiling of a square, each tile has rational proportion to the whole square. This is true, but certainly not easy to prove. So it certainly isn’t obvious. It is directly answered in this post on stackexchange:
http://math.stackexchange.com/questions/14878/cutting-a-unit-square-into-smaller-squaresThere is a website devoted to this sort of tiling, http://www.squaring.net/index.html. A good historical summary is given in this pdf:
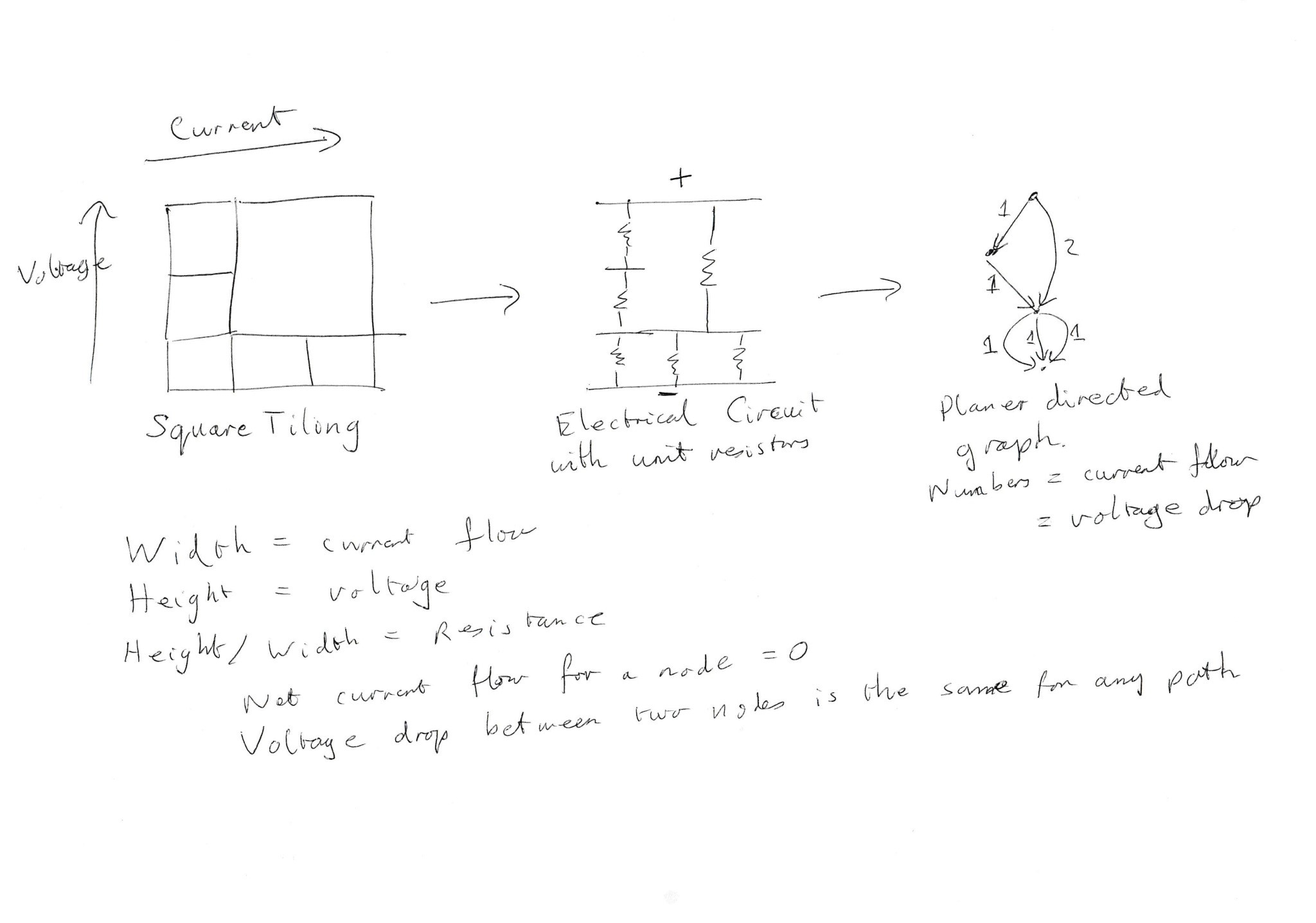
http://ime.math.arizona.edu/ati/Math%20Projects/C1_MathFinal_Papenfus.pdf.After Dehn the main progress was made by noting that a rectangular tiling of a rectangle is equivalent to an electrical circuit involving only resistors. This, maybe, gives a more comprehensible proof of your conjecture.
In general width represents current flow and height represents voltage. A square has unit resistance since the ratio of voltage to current is 1.
We imagine that the tiled rectangle represents a circuit with a voltage applied between the top and bottom edges. Each rectangle is a resistor, allowing current to flow between it’s top and bottom edges. The current flow through each rectangle is the width, and the voltage drop is the height. Horizontal lines are electrical connectors, connecting the resistors above to the resistors below.
We note that the current flowing into each node (horizontal line) is equal to the current flowing out. In other words the combined width of the squares above a horizontal line is equal to the combined width of the squares below it.
The voltage drop between any two nodes is the same whichever path is taken, since this is just the difference in the height of the two nodes. Note that a square represents a unit resistor, since the voltage drop and current (height and width) are the same.
A simple example may help:



I think this boils down to the question, “Can all rectangles be cut completely into squares?” It seems trivial to ask if they can be cut into triangles, because you need only cut diagonally, but squares have more requirements. If you cut a square off of a non-square rectangle, even the largest square possible, are you left with a question any different but with a smaller shape?
If r is a rational number, it stands to reason that r and (1-r) will have a rational least common multiple. If the initial unit square can be cut into a checkerboard of squares of that size, r² will exist and only squares will remain.
I agree that if r is rational, the tiling is definitely possible, for the reasons you state. However, can we prove that it is impossible if r is irrational? I have some ideas, but no obvious argument as yet.
This puzzle made me think of Stan Wagon. He made his name as a young man with… [FULL COMMENT REPRODUCED IN POST]
This looks tremendous. Thanks for the effort that you have put in here. I certainly don’t fully understand it all yet, but I will have a good look through and try to work it all out. It’s good to know that (a) my intuition was right and (b) I was not asking a foolish question. It also looks like there is some fascinating maths involved.
Superb.