This rather elegant fact has been going round on Twitter:
“It can’t be true … can it?” Rachael Formula. More info/discussion: http://t.co/gh6Lt76si1 pic.twitter.com/sDc547kEyV
— Cliff Pickover (@pickover) April 15, 2015
r
However, there are other examples of this phenomenon…
@pickover @Derektionary This has not been unknown to the dabbler in such matters. The number 3 and 3/8 behaves in a parallel fashion.
— Chris Maslanka (@ChrisMaslanka) April 15, 2015
r
i.e.
In fact, pleasingly, we can construct an infinite number of facts like this.
Let’s say that we want to find positive integers A, B and C, such that:
√(A + B/C) = A √(B/C) [1]
We can also suppose that B < C (otherwise our mixed fraction would be a little odd) and that the highest common factor of B and C is 1, so that the fraction B/C is in its lowest form.
To find a relationship between A, B and C, we can square [1] and rearrange the equation to get the A terms on one side:
___________________________[1] ⇔ A + B/C = A² (B/C)
_______________________________⇔ A = (A² – 1) (B/C)
_______________________________⇔ A/(A² – 1) = B/C , A > 1 [2]
We can use double implications (⇔) here since we know that everything is positive.
Now, [2] tells us that two fractions with positive integer numerator and denominator are equal. Both fractions are in their lowest form (B/C because we said so earlier, while A and (A²–––1) clearly have a highest common factor of 1). Therefore the numerators and denominators are equal:
[2] ⇔ A = B and A² – 1 = C (if A > 1)
This means that there is an infinite family of solutions of the form:
Any integer greater than 1 will do as a value for A, so we have:
and so on…
Rather nice.
Click HERE for another investigation of a maths tweet from Cliff Pickover.

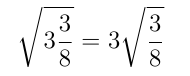
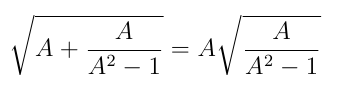
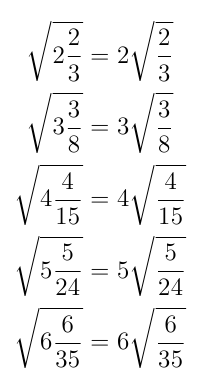
In these examples there should be a “+” symbol between the integer and the fraction that appear under the radical. Some one should correct this!
It is implied summation on the left hand side, following the (somewhat idiosyncratic) convention of how mixed numbers are presented, but implied multiplication on the right hand side, following the convention of everything else in mathematics. I think it is correct as stated.
Pingback: Mixed Number Curiosity | CAS Musings